Studentům: výpočty kružnice v EUKLIDOVĚ PROSTORU
| ○ OBVOD kružnice [m]
|
O = π
· d = 2 · π · r
|
| ● OBSAH
kružnice [m2] |
S = π
· d2/4 = π
· r2 |
d … průměr kružnice [m] r
… poloměr kružnice [m]
Iracionální Ludolfovo číslo (pí) … π
= 3,1415926535897932384626433832… [–]
Poznámky:
 π Upřesňuje se jeho nejsoucí velikost; výpočet zůstane nepřesný
○ Kružnice je tvořena všemi body, jež mají od jejího středu vzdálenost zvoleného poloměru
● Kruh navíc obsahuje i všechny body, jež kružnice v sobě uzavírá
π Upřesňuje se jeho nejsoucí velikost; výpočet zůstane nepřesný
○ Kružnice je tvořena všemi body, jež mají od jejího středu vzdálenost zvoleného poloměru
● Kruh navíc obsahuje i všechny body, jež kružnice v sobě uzavírá
Žijeme virtuální realitou
Perspektivní zrakový prostor - matematika
Výpočet obvodu kružnice - XII 💾

Bohumír Tichánek
* * *
Málokdy sledujeme rozpor mezi zrakovými a hmatovými zážitky.
Zrakové - stlačované perspektivou, a nebo hmatové - lineární
(rovnoměrné)? Jsou-li základem poznání světa informace - poznatky, pak
jen jeden ze zážitků vystihuje skutečnost našeho světa.
Od starších generací přebíráme názor, že smyslové zážitky jsou tvořené
tělesy z Euklidova rovnoměrného prostoru. Námitka - představu lineární délky okolí při chůzi, tedy vliv hmatu, lze nahradit. Navíc - hmat
naprosto nepředává to ohromné množství současných informací [bit] oproti zraku.
Jaká geometrie podkládá náš svět? Ve starověku byla promyšlena lineární
Euklidova geometrie; jenže v ní nikdy nevypočítáme obvod kružnice. Proto lze váhat nad skutečností hmotného Euklidova světa, když výpočty
ji nepotvrzují!
Délku obvodu kružnice vyjadřuje iracionální výsledek: vždy nepřesně v Euklidově prostoru. Člověk si z počítaného výsledku vybere svou hodnotu - nějaký počet desetinných míst. Geometrická délka je konečná, kdežto dva lidé musí dohodnout, kterou délku zvolit - např. kolik desetinných míst. Rozpor zpochybňuje lineární geometrii světa.
V dalším se vracím do nejzákladnější geometrie, vnímané zrakem.
Tu lze odvozovat z diskrétního prostoru. Bude praktický význam postupu,
vycházející z biologické podstaty člověka, nalezen později?
* * *
OBSAH
- Seznam symbolů
- Kružnice tří prostorů
1.1. Euklidův prostor
1.2. Diskrétní prostor
1.3. Perspektivní prostor
- Posouzení obvodu kružnice
- Délka obvodu v perspektivě
- Závěr
0. Seznam symbolů
O … obvod kružnice diskrétního, Euklidova a perspektivního prostoru
d … průměr kružnice. V diskrétním prostoru též úhlopříčka a strana čtverce, postaveného na vrchol
r … poloměr kružnice
1. Kružnice tří prostorů
1.1. Euklidův prostor
V lineárním Euklidově prostoru zjišťujeme
obvod kružnice O nepřesně. Průměr d násobíme iracionálním - neohraničeným
Ludolfovým číslem π.
O = π · d
Obvod nevypočítáme. Spokojujeme se s údajem, jehož přibližnost
předepsalo zaokrouhlení čísla π. Dosavadní teorie dbá názoru, že nelze zjistit konečnou délku obvodu; vyjádřit ji racionálním číslem.
Nemožnost výsledku jednoznačné velikosti označuje iracionálním číslem.
Lze hledat, zda tytéž poznatky platí i v každém jiném prostoru.
Ačkoliv kružnice má konečnou délku obvodu, konečný (racionální) výsledek nezískáme.
Příčina existence iracionalit je kupodivu opomíjená.
Sleduji ji v preferovaném Euklidově (lineárním spojitém)
prostoru. Iracionality zpochybňují Euklidův prostor jako geometrii,
která by popisovala rozložení hmoty v našem světě.
1.2. Diskrétní prostor
V diskrétním prostoru (obdoba šachovnice) se délky posuzují počtem
kroků (obr. 1 - Diskr.). Vzdálenost ke každému červenému bodu, ze středu čtverce [0, 0], je stejná. Užitý bodový obrazec vyhovuje definici kružnice. Čtverec, postavený na vrchol, je kružnicí diskrétního prostoru.
Průměr obrazce činí 6 kroků (od -3 až do +3). Také krokování čtvrtiny obvodu vytvoří 6 červených úseček. Celý obvod vyžaduje 4×6, to je 24 kroků.
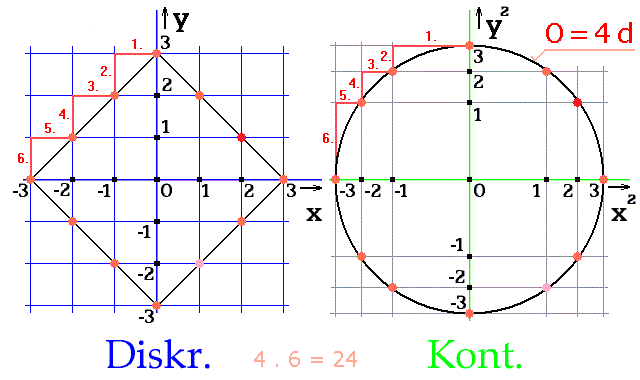
Obr. 1. Obvod daný počtem kroků v diskrétním a v perspektivním prostoru
««« SLEDOVAT VŠECHNY OBRÁZKY I V LEVÉM SLOUPCI
1.3. Perspektivní prostor
Perspektivní
prostor vystihují osy, které cejchuji druhou mocninou přirozených čísel (obr. 1 - Kont.). Další
souvislosti s hledáním, jež by vystihly geometrii perspektivy, sleduji
v jiných textech.
Převodem bodu, z diskrétního do perspektivního prostoru, mu zůstane
stejná vzdálenost od počátku a stejné souřadnice x, y. Například bodu N [2, 1] činí vzdálenost vždy d/2 = 3 (obr. 2 Diskr., Kont.). Leží na kružnici o poloměru 3.
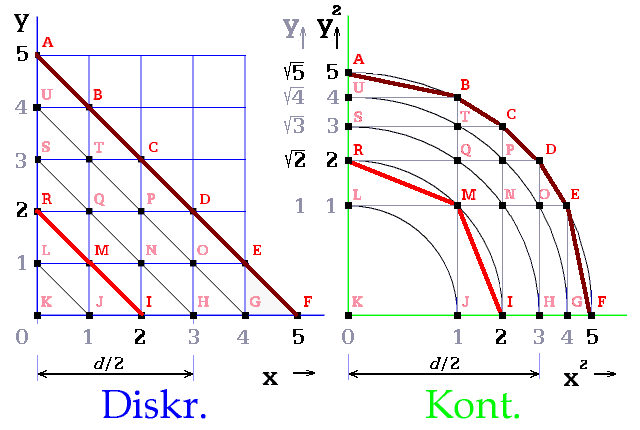
Obr. 2. Kružnice rostoucího průměru
Kružnice je v perspektivě předurčena počtem kroků v diskrétním
prostoru. Z něho přebírám výpočet kružnice v perspektivě. Diskrétní prostor zajišťuje absolutní přesnost výpočtu.
V perspektivě vzniká z bodů kružnice; rovněž o průměru d = 6 (obr. 1). Konstrukce užívá tří
různých délek úseček, jimiž napodobuje kružnici. Tyto tři červené
úsečky (obr. 1 - Kont.) jsou označené 1. (délka
0-1), 2. (délka 2-3 ) a 3. (délka 1-2). Obvod
kružnice je zde čtyřnásobkem jejího průměru: O = 4·d. Tento
výpočet obvodu nepotřebuje žádné iracionální číslo.
To proto, že rozměry se vyjadřují přirozeným počtem kroků. Výpočet útvaru konečné délky je tímto konečný.
Útvar jakoby zůstával v diskrétním tvaru. Diskrétní kroky oblé
kružnice - segmenty - se však různě liší svou délkou. Lze rozvážit,
zda je tento prostor kontinuální či nikoliv. V grafu lze dohledat
původní body, proto se nabízí i hodnocení: pseudokontinuum.
Kružnice obvyklé velikosti nemívají tak malý průměr (obr. 1),
nýbrž s přihlédnutím k Planckově délce je tvoří například 1035 bodů. Planckova čísla upozorňují na nespojitost našeho světa. S růstem průměru se pseudokružnice zaobluje (obr. 2).
Lidský zrak nerozeznává podrobnosti a následně kružnice posuzujeme jako spojité kulaté.
|
1. Poznámka: Pozorovatel je v počátku souřadnic [0, 0].
Začne se otáčet (obr. 1), a přitom ať pozoruje body rozložené na kružnici poloměru např. r = 3. Zjistí snad, že dvojice
sousedních bodů mají různou vzájemnou vzdálenost? Tato nelinearita snad nějak souvisí se zážitkem vycházejícího Měsíce -
jenž se postupně zmenšuje?
Nelinearitu lze vyloučit jiným rozložením bodů na každé kružnici. Určí je matematika, tudíž je takový postup nadějný. Bude však
náročnější, než jsou pouhé návrhy mechanických modelů.
|
2. Posouzení obvodu kružnice
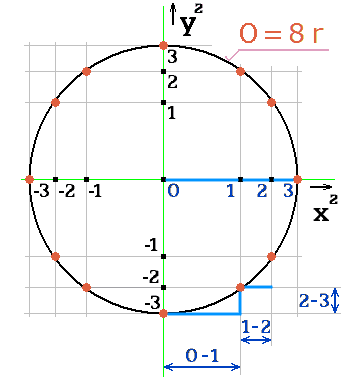
Obr. 3. Obvod daný osminásobkem poloměru v perspektivním prostoru
I pro perspektivní prostor platí d = 2·r (obr. 3). Posoudím vzorec obvodu: O = 4·d = 8·r.
Poloměr zvolené kružnice r = 3, to je 0 až 3, zahrnuje délky 0-1 a 1-2 a 2-3 například na vodorovné ose. Snadno
ověřím, zda se tyto délky nalézají skutečně na obvodě kružnice.
Vpravo dole jsou vyznačené kroky. Jsou to červené úsečky v délkách 0-1, pak 2-3 a 1-2. Na obvodě kružnice se tato
trojice vyskytne 8×. Žádnou nesnáz neobjevuji, vzorec O = 8·r vyhovuje.
3. Délka obvodu v perspektivě
Vzniká otázka - k čemu je takový výpočet obvodu dobrý?
Vždyť kdybychom kruh obtočili provázkem a ten pak rozvinuli…
|
2. Poznámka: Na otázku ihned odpovídám, když právě takové se objevují. Bodový
prostor, přepočítávaný do perspektivy, svědčí o umělé, promyšlené
konstrukci našeho světa. Stejně tak pulsní zdroj podle teorie relativity, jenž dovolí zpomalovat čas…
|
Obvod kružnice obtočím provázkem délky O = 24 kroků.
Pak jej natáhnu na vodorovnou osu (obr. 4).
Nejprve mezi body 0 ↔ 24 (fialová šipka). Pak mezi body 1 ↔
25 (modrá šipka). Je to stále stejný provázek o délce 24 kroků. Už
délka fialové šipky vyhrožuje, že tento provázek by nestačil na obtočení kružnice; natož jeho modrá verze.
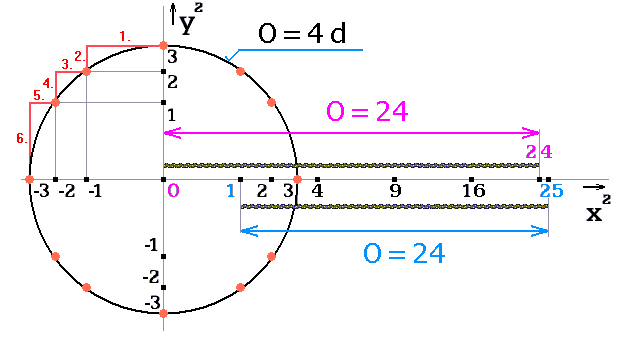
Obr. 4. Porovnání obvodu kružnice a obemykajícího provázku
Takovou situaci známe z denního života. Při vzdalování provázku je
pohled na jeho zkracování samozřejmý. Lidský vjem se shoduje s odlišnými délkami v obrázku.
Zkouším zdůrazňovat vliv perspektivy.
Tento text hledá, zda lze náš svět posuzovat
jako projektovaný, zkonstruovaný a nakonec nyní provozovaný. Zdůrazňuji vnímané
zážitky a hledám, zda jsou podložené nadřazenou Informatikou. |
Rozhodující je, zda vyhovuje
matematické řešení. Tentýž provázek, umístěný v jiných místech
roviny, vždy výpočetně splňuje délkový požadavek. Jeho skutečnou
délku ať určuje diskrétní prostor. V perspektivním prostoru se
toliko promítá stlačované zobrazení, jehož zdrojem je diskrétní
prostor. Přenos, přepočet vnáší do smyslového vnímání nestejné délky.
Vnímaná úsečka mění svou délku podle vzdálenosti od počátku.
Absolutně přesné řešení v perspektivním prostoru je podložené
diskrétně (bodově). Kdežto hypotetický Euklidův prostor, s Ludolfovým číslem
π, je uměle matematizovatelný až zavedením „iracionálních čísel“ - ad hoc
(= právě pro tento případ, jen k tomuto účelu).
Perspektiva neužívá
Euklidova prostoru a vidění nepodmiňuje zorným úhlem. Úctyhodně starověký prostor neskutečných a iracionálních vzdáleností, našemu světu, odmítá.
| Iracionality vznikají převodem kvadraticky
rozmístěných souřadnic do lineárního měřítka. Vznikají následkem
snahy převést vnímané obrazy, jež objevujeme ve svém vědomí, do
fiktivního lineárního prostoru. |
Lineární prostor si zdůvodňujeme v denním životě. Kráčející chodec má
každý svůj další krok stejně dlouhý, vždy znovu první; proto máme za to,
že prostor je lineární. Totéž však splňuje i svět perspektivní komprimace - i středovému
pozorovateli je každý další krok první, stejně dlouhý.
4. Závěr
Použitý přístup zdůrazňuje význam perspektivního
prostoru. Odmítnutím iracionalit nabízí, že zřejmě jen pouhé počty upřesňují
podstatu našeho světa. Nedopočítatelné výsledky nahrazuji jednoduššími
postupy. Až budoucnost ukáže, zda
absolutní přesnost - odvozená z diskrétního prostoru - by měla svůj
smysl při výpočtech kružnice. Nýbrž zde uvedené názory sledují něco
jiného - názor na konstrukci Vesmíru.
Pro výpočty kružnice i koule používáme iracionálního Ludolfova
čísla π.
Pro zpřesnění výsledku použijeme třeba i obrovského počtu desetinných
míst. Snaha o přesnost může být i nepotřebná, například s 101.000.000 desetinnými místy. Předpokládám, že nejpřesnější
výsledek lze získat úsporným postupem. Počet nutných desetinných
míst spojitého prostoru odvodit z počtu diskrétních kroků,
připadajících na jednotku délky.
Převod z diskrétního do perspektivního prostoru, s užitím Planckovy
délky, dbá absolutní přesnosti. Lze si představit, že v budoucnosti
budeme řešit ve hmotě takové úkoly,u kterých rozhodne přesnost
výpočtů. Například pro určení krouživého pohybu nebezpečných meteoritů,
se započtením mnoha vlivů a to dlouhodobě.
|
Euklidův prostor: Obvod kružnice je nevypočítatelný, protože Ludolfovo číslo je iracionální.
Jenže konečná délka obvodu, určená geometrií, vyžaduje racionální výsledek.
Nevyčíslitelná délka odmítá rozložení hmoty v Euklidově prostoru.
|
|
Perspektivní
zrakový prostor odvozuji z diskrétního.
Po převodu bodu do druhého prostoru mu zůstanou stejné osové souřadnice a stejná vzdálenost od počátku. |
|
Perspektivní prostor: Velikost obvodu je určena počtem bodů diskrétního prostoru. Obvod je tak vyjádřený racionálním číslem - přesně.
V perspektivě, při vzdalování pozorovatele od kružnice, se mu zmenšuje její velikost a mění tvar. Avšak vyčíslená délka obvodu se nemění; počet bodů - segmentů zůstává stejný.
|


