Pochybnosti o geometrii vesmírného prostoru - I


verze 1. 1. 2019a
Bohumír Tichánek
* * *

Bohumír Tichánek
* * *Mysl nebéře zákony z přírody, nýbrž sama jí je předpisuje [1]
Immanuel Kant (1724 - 1804)
| Matematické iracionality nevystihují geometrii. Prozkoumáním detailů se blížíme skutečnosti, nikoliv jejich zanedbáním. Vždy vidíme perspektivní prostor, nikdy Euklidův. |
OBSAH
Nejdůležitější součástí budovy bývá střecha? Nejvíc trpí podnebím a její zničení pak poškodí celý dům. Jenže neopomeňme základy domu. Ty se však málokdy bortí, takže si jejich důležitost neuvědomíme. Dávno jsme přijali varování před stavěním na písku; již na ně ani nemyslíme.
Těmi základy domu, ve fyzice, je prostor (obr. 1).
Matematika může používat různých svých prostorů a postupů podle libosti, a
ony nemusí souviset s vesmírnou skutečností. Naopak fyzika ověřuje své názory experimenty.
Dbá skutečnosti a tím bývají její výsledky pro svět důležité. Má vysvětlit, kde žijeme;
a to i jiným postupy než právě matematickými výpočty.
Časoprostor podle Minkowského má dvě složky; z nich prostor můžeme zkoumat snadněji než čas. Euklidův prostor byl popsaný již před tisíciletími, kdežto až ve 20. století fyzika našla závislost času na rychlosti pohybu.
Předkládám výhrady vůči dlouhodobému názoru na geometrii
fyzikálního prostoru. Nabídnu jinou možnost.

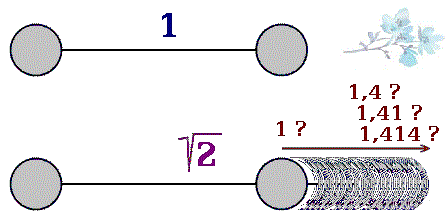
Zjistěme úhlopříčku čtverce, když délka strany je a = 1. Počítat můžeme ze zadané délky Pythagorovou větou, v pravoúhlém trojúhelníku: a2 + b2 = c2. Jenže výpočet nikdy neskončí (obr. 2). Ani nejrychlejší počítač se výsledku nepřiblíží. Zaokrouhlením výsledku na nějaký počet desetinných míst se smíříme s chybou; zanedbáme ji.

Považuji za správné, za nejlepší, moci zadat práci klempířovi tímto způsobem. Vyrobte čtverec o straně 1 m, a pro kontrolu - jeho úhlopříčka bude tolik a tolik. Například bych mu chtěl bez obav říct: Jeho úhlopříčka bude přesně 1,4 metru. A to bez zaokrouhlení. Nejsem spokojen s poznáním světa, které nedovede zdůvodnit, proč se přepočet Pythagorovou větou nedaří. Zadám-li úhlopříčce 1,41 metru, pak klempíř možná ani neví, že údaj je zaokrouhlený. Skutečně to vysvětlit nikdy nepůjde?
Konstruktér musí předem ohlídat, aby si klempíř nerval vztekem vlasy. Délku strany čtverce výroba dodržela s přesností lepší než desetina milimetru, a přece v úhlopříčce 4 mm přebývají. Čtverec, zadaný stranou 1,000 metru, má úhlopříčku délky 1,414 metru - při zaokrouhlení na tisíciny.
Klid - konstruktér, opatrně a moudře, neudává všechny rozměry výrobku a zadává i toleranci. Tento vymyšlený příklad není příčinou mých snah. Nýbrž mi jde o poznání světa. Horolezci lezou na vrcholy hor proto, že ty hory jsou. Podobně zvláštnost ve výpočtech délek světa se snažím prohlédnout proto, že je. Nejprve si mužové hráli s rozkladem světla do barev duhy. Až později se ukázalo, že bylo prospěšné prostudovat způsob průchodu světla sklem. Že lze vyrobit nejen okenní tabuli, ale i optický dalekohled a mikroskop. Objevit měsíční krátery a bacily.
Popisovaný rozpor iracionalit je problémem méně pro techniku a víc
pro filosofii či snad pro nauky o vytvoření světa, kromě matematiky.
Hledání patří exaktním oborům - fyzice, matematice. Snad proto
tyto obory dříve patřívaly do filosofie. Dnes však takové zařazení
chápeme jako paradox - dnes hledající fyzika poněkud dbá
požadavků techniky a ta zase obchodu.
Rozlišuji, ve kterém oboru vědy prostor uvažujeme. Zda v matematice nebo ve fyzice. Obrátím-li se s nějakými názory ohledně iracionálních čísel na matematika, bude můj přístup poměřovat svými postupy. Ty dávají prospěšné výsledky. Matematika popisuje prostor reálnými čísly. Zahrnují jak racionální (např. 7 nebo 5,64 nebo 1/8), tak nepřesná iracionální čísla (π nebo odmocnina ze dvou nebo e - základ přirozených logaritmů) - čísla nejsoucích velikostí.
Jak naměřit délku úhlopříčky jednotkového čtverce, shodnou s výpočtem? Pro stranu a = 1
sděluje Pythagorova věta u = √2. Vypočítanou odmocninou může
být 1 nebo 1,4 nebo 1,41 nebo 1,414 atd.
(obr. 3). Podle požadované nepřesnosti využijeme jen potřebný
počet desetinných míst. Sleduji myšlenkový postup, nikoliv měření
délky posuvkou nebo laserem. Nestačila by mi ani přesnost zaručená na
jakýkoliv počet desetinných míst.
Iracionální čísla jsou oporou vyšší matematiky, tudíž matematik
stěží porozumí mým pochybnostem. Vždyť získává své výsledky.
Jejich porovnání se skutečností našeho světa je již jiným
oborem - fyzikou. Euklidův prostor je určený matematickými
postupy a k tomu nemusí být provedený ve Vesmíru. Matematika,
obohacená o iracionální čísla, je prospěšná, ale přitom Euklidův
prostor nemusí být skutečností fyziky.
Fyzika bádá nad vesmírnými záležitostmi. K tomu užívá experimenty a
přijaté závěry mají být s nimi v souladu.
Fyzika pracuje s prostory, o kterých si nejsme jistí, zda vůbec
můžou být, zda jsou skutečné. Uvažuje prostory čtyřrozměrné (4D) či 5D a ještě více
rozměrné, i když je možná ve Vesmíru nenajdeme (obr. 4).
Hluboce přemýšlené (přemyšlené) názory zavádějí nevnímané rozměry
- nějak svinuté. Protože se používají jen ve výpočtech, pak k rozporu
nedochází. Strunová teorie nedává závěry k experimentálnímu ověření.
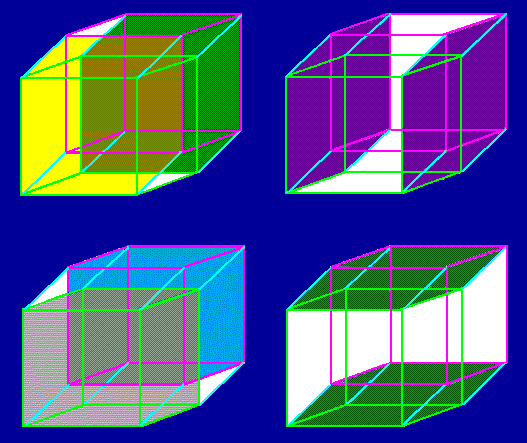
Matematika nepotřebuje posuzovat, zda její používané prostory ve Vesmíru existují. Uplatňuje potřebné rovnice vyššího řádu. Avšak kam směrovat čtvrtou kolmici v našem prostoru, chceme-li v mechanickém modelu uvažovat 4. rozměr? V našem 3D prostoru máme tři kolmice, u kterých každá dvojice svírá úhel 90°. Kdežto 4D prostor má mít i čtvrtou kolmici, která opět má svírat úhel 90° proti ostatním třem kolmicím. To nám dosud ve Vesmíru nikdo neukázal.
Kam mířím? Tak jako fyzika svými výpočty pracuje s vícerozměrnými prostory, stejně tak pracuje s Euklidovým prostorem nebo s prostory od něj odvozenými - zakřivenými. Není zaručeno, že vyjmenované prostory existují. Uvažuji zde nad nejistotou existence světového Euklidova prostoru. Jak jedenáctirozměrný, tak Euklidův 3D prostor pouze předpokládáme. Vždyť zrakem zjišťujeme prostor jiný, stlačený perspektivou. Ovšem to je „pouhý smyslový zážitek“.
Zkouším prověřit 3D Euklidův prostor tam, kde výpočet nedává racionální řešení. Přitom matematika neselhává, řeší bez chyby. Zaručuje, že výpočet desetinného vyjádření iracionálního čísla bude vždy bez konce.
Prostor k pokroku hledám v geometrii.
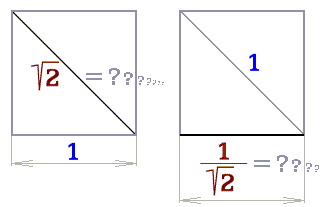
V Euklidově geometrickém prostoru vyjadřujeme tu samou
1D délku jedním a jindy druhým obvyklým způsobem (obr. 5).
Změříme stranu čtverce, zadáme ji do výpočtu a výsledkem je úhlopříčka
vždy iracionální. Nebo naopak - ze zadané změřené úhlopříčky vyplývá
iracionální strana. Délky strany a úhlopříčky jsou nesouměřitelné;
je-li jedna racionální, pak druhá je vždy iracionální. Tato mnohost
vede k pochybnosti, zda je to v úplném pořádku. Váhám nad
prostorem, který vyžaduje dva druhy vzdáleností. Je to konečná
pravda? Bylo by lepší, kdyby této zdvojenosti nebylo. Vhodnější by
bylo vyjadřování délek jen racionálními čísly - jenže jak to
zajistit?
O složitostech je známo: „Velké objevy ve fyzice jsou proto velké, že redukují počet postulátů potřebných na popis světa na nejmenší počet. To je při hledání nových poznatků nejvlastnější funkce vědy.“ [2]
Zde toliko připomínám nutnost pochyb nad složitostí.
Kvalitativně se dvě úsečky v Euklidově prostoru neliší,
vždy jen kvantitativně - proč tedy dva druhy čísel?
Pythagorovu větu vykládám obrázkem se čtvercovou sítí (obr. 6).
Soudíme, že dva menší čtverce dohromady mají stejný obsah, jako má velký čtverec:
(1 + 2) + (3 + 4) = 1' + 2' + 3' + 4'
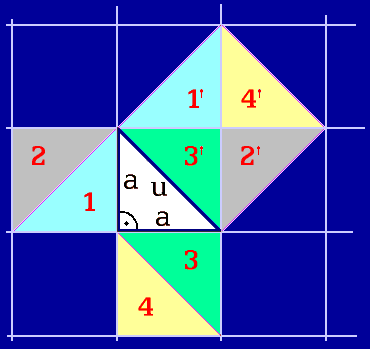
Obr. 6. Pythagorova věta v síti
Je snad v rovině vidět shoda devíti stejných trojúhelníků? Sleduji 1', 2', 3', 4', 1, 2,
3, 4, aua.
Jestliže máme oči přímo nad středem obrázku, pak vzdálenější místa se zmenšují vlivem perspektivy. Zrak nepotvrdí shodu povrchů, vždyť perspektiva ukazuje obrazce v rozdílných velikostech. Perspektivní zkreslení ve svých zážitcích zřejmě nevnímáme, neuvažujeme nad ním. Promyšlením svého zrakového zážitku můžeme uznat, že shodnost nevidíme a jen ji předpokládáme. A výpočetní prověření vede k nekončícímu výpočtu. Častý výsledek přepočtu z 2D do 1D prostoru se hodnotí dohodnutým způsobem - iracionální délku zaokrouhlíme.
Pythagorovu větu náš zrak nepotvrdí.
Hmat zaručí skutečnost? Chodec, jako středový pozorovatel, má každý další krok opět první. Sám zůstává středem stlačených souřadnic perspektivního prostoru. Je nebo není tím šizen, chce-li přísahat, že svět je mu daný lineárním rozložením hmoty?
Je paradoxní, že odmocnina ze dvou je současně číslem - iracionálním, a současně pokynem k hledání čísla: hledej číslo x, které násobené samo sebou, dává dvě! Tedy v rovnici:
Výpočty poukazují na Euklidův prostor iracionální - neskutečný.
Jak smyslový zážitek - pohled, tak ani matematika nedávají výsledek, který by potvrdil skutečnost Pythagorovy věty.
Při hledání souvislostí iracionálních čísel v geometrii pátrám po jiném, lépe vyhovujícím prostoru.
Zajímavý je názor Ernsta Macha (1838 - 1916), dávno zesnulého rakouského fyzika původem z Moravy. Měl za to, že zvláště fyzika získá největších vysvětlení od biologie, a to analýzou smyslových počitků. Vycházel z názoru, že objektem vědy jsou komplexy počitků, které nemají objektivní příčinu [3]. I v kvantové mechanice lze uvažovat Machovým způsobem.
Matematika vznikla ze smyslových zážitků. I když až jejich abstrakcí. Fyzikální poznatek o teplotě hrnku s vřelou vodou lze někdy zjistit i bez přemýšlení, kdežto zjistit počet hrnků vyžaduje abstrahovat.
Zjišťuji jakousi nesnáz pro závěry filosofa K. Poppera (1902 - 1994)
- o vyvratitelnosti. Na jedné straně bývají smyslové zážitky podrobené chybám. Hledíme na
obraz rovnoběžek, ale máme pocit, že jsou to různoběžky
(obr. 7). Změřením se chybný názor vyvrátí. Vliv šálivé
podrobnosti u každého čtverce lze pochopit a zneškodnit.
Rozmístění rohových černobílých čtverečků zdánlivě ohýbalo čáry.
Nejmenší detaily určují naše rozhodnutí. Teprve prozkoumáním detailů se
blížíme skutečnosti, nikoliv jejich zanedbáním.
Z prostoru mezi dvěma reprobednami slyšíme zvuk, takže tam
uprostřed musí být jeho zdroj - věděl by se zavřenýma očima dávno
odešlý Mozart (1756 - 1791).
Přece je jinde! Exaktní poznání opraví zážitky, které smysly chybně
vyhodnotily. Ale tím nevyvrací tyto smyslové poznatky. Vždyť
dvojice uší s mozkem prověřují zdroje signálu a pak upřímně
informují naše vědomí, že zvuk přichází z prostoru mezi
dvěma zdroji. Zvukové signály se sečetly.
Příště může posluchač hodnotit totožnost zdroje opět nesprávně, pokud budou nastražené falešné reprobedny, schválně přichystané k jeho zmýlení. A zdrojem bude naopak - skrytá jediná reprobedna uprostřed.
Zajímám se o vědou nedoceněný prostor, který je obsažený v
našich smyslových zážitcích. Na perspektivní prostor může člověk přísahat, neboť jej vnímá.
Smyslové zážitky jsou ovšem nevědecké tím, že jsou zřejmě
nevyvratitelné! Nejen každodenní zážitky sluchu, zraku, čichu,
chutě a hmatu, ale i jejich pokřivené odvozeniny vnímáme jednoznačně.
Poživačům drog se zrakové zážitky můžou prohýbat. Popisem skutečnosti
nejsou, ale zřejmě jsou nevyvratitelnými zdroji informací.
Věda opravuje svými vysvětleními až chápání zážitků.
Vidí-li opilec bílé myši, pak mu
nikdo nevyvrátí, že vidí bílé myši. A přitom může souhlasit, že
nejsou skutečné. Smyslové poznatky jsou vysvětlitelné, ale člověk
je zpracovává po svém. Nedoceňujeme je.
Spící člověk obvykle bývá přesvědčený o skutečnosti svého
snového prožívání; až po probuzení pochopí jeho neskutečnost. Nad
nočním snem mávneme rukou - a podceníme upozornění, souvislost s denním
životem. Žebřík nemívá jen jednu příčku a vždy je obousměrný.
Filosof Karl Popper prosadil, že předpokladem vědeckého pokroku je vyvratitelnost přijímaných poznatků. Nevyvratitelné názory věda nejen odmítá, ale někdy jimi lidé i opovrhují.
Jenže naše nevyvratitelné smyslové zážitky jsou základem veškerého poznání.
Kde, v jakém prostoru hledáme zdůvodnění fyzikálních poznatků? Kde hledáme svůj život?
„Co tu děláte?“
„Hledám klíče. Někde mi v kuchyni vypadly.“
„A proč je hledáte tady na dvorku?“
„Protože venku je světlo, v kuchyni mám tmu!“
Závěr proslulé historky sděluje Osho:
Rábi'a řekla: „Myslíte si, že jsem blázen, a přitom po celý život děláte přesně tohle - a nejste blázni? Kde jste ztratili sebe a kde se sami sebe snažíte najít? Kde jste ztratili svou blaženost a kde se ji snažíte najít? Ztratili jste ji ve svém vnitřním světě, ale hledáte ji venku!“ [4]