Pojmy

Diskrétní prostor - obsahuje rozlišené body. Jejich souřadnice jsou výhradně celočíselné a vzdálenosti se určují počtem svislých a vodorovných kroků. Délka kroku se nehodnotí, jen počet. Takovým prostorem je i šachovnice.

Perspektivní prostor - je daný zrakovým i sluchovým vnímáním člověka.

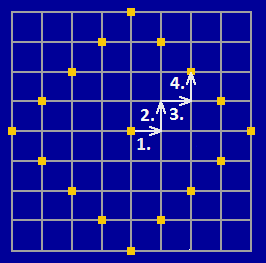
Obr. 1.

Diskrétní prostor. Počet kroků určí vzdálenost mezi dvěma posicemi.

V 2D prostoru má posice právě jiné čtyři posice sousední, do kterých lze bod přesunout jedním krokem (taximetrika): nahoru, dolů, vlevo, vpravo.

««« SLEDOVAT VŠECHNY OBRÁZKY I V LEVÉM SLOUPCI

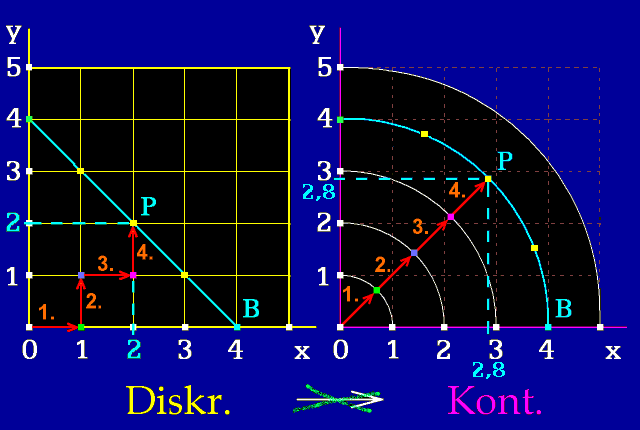
Obr. 2.

Má-li jistý bod (P) stejnou vzdálenost od počátku v diskrétním a v Euklidově prostoru, pak ale nemá stejné souřadnice. Výjimkou jsou jen body (B), které leží na osách x a y. Tudíž diskrétní prostor neposlouží jako skladiště bodů pro přepočet do Euklidova prostoru.

Obr. 3.

Lze přepočítat body z posic diskrétního prostoru, tentokrát do kontinua kvadratického prostoru?

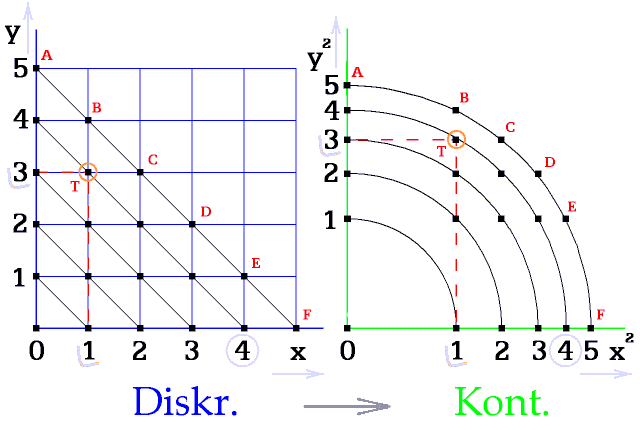
Obr. 4.

Bod T [1, 3] je od počátku [0, 0] vzdálený 4 kroky. Vzdálenost 4 má v prostoru diskrétním, a stejně tak v nabízeném kontinuu. Také kartézské souřadnice [1, 3] má v obou prostorech stejné.

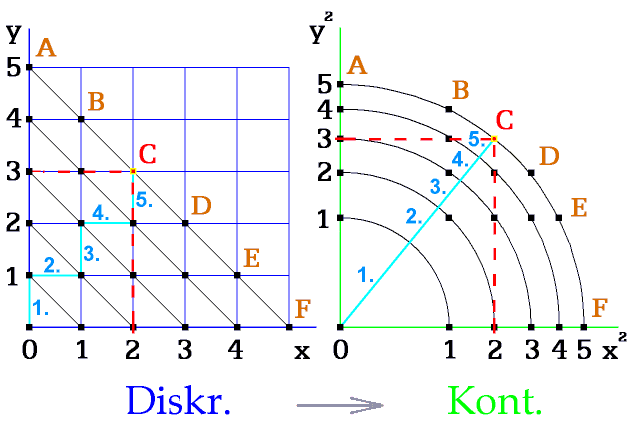
Obr. 5.

Převod bodu C [2, 3] mezi oběma prostory. Prostor s kvadratickým cejchováním os navazuje na diskrétní prostor a touto spoluprací se podstatně odlišuje od Euklidova lineárního prostoru.

Slučitelnost prostorů nabízí možnost: chod Vesmíru se odehrává v diskrétním prostředí a z něho každý tvor dostává, do svého vědomí, informace o umístění hmoty. Přepočítané ve prospěch zrakového vnímání. Další matematická úprava kvadratického prostoru směřuje k optimálnímu vystižení zážitků perspektivy.

Tvor je vždy umístěný v počátku souřadnic, odkud vnímá prostor perspektivně rozložený.

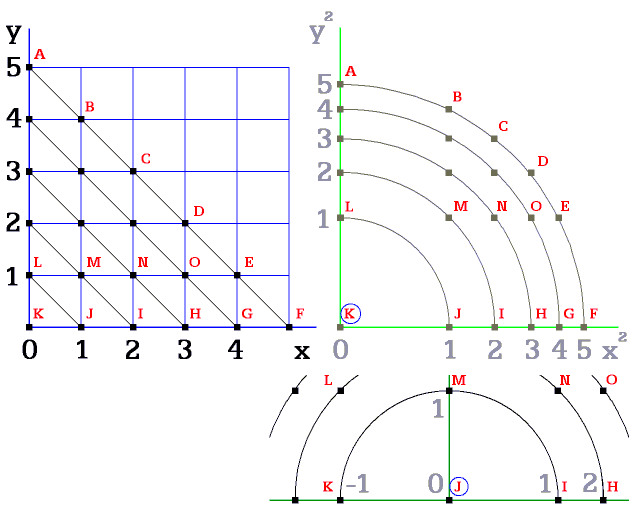
Obr. 6.

Zobrazení situace tvora - pozorovatele ve světě. Jako ideální kružnice vidí právě ty, které mají střed v počátku. Počátkem je mu vždy ta posice v prostoru, na které se právě nalézá on sám.

Ať obsazuje kteroukoliv posici prostoru, např. bod K, potom J, vždy zjišťuje svůj první krok o stejné délce. Z toho získává základní názor, že celý svět je lineární. Jenže správnost takového názoru na světový prostor ať posoudí úspěšná matematizace. A to bez zavádění iracionálních čísel ad hoc - vždyť nemají určitou svou velikost.

V lineárním Euklidově prostoru se někdy nabízejí iracionality. Tehdy není délka jednoznačně určená, narozdíl od smyslového zážitku. Řešitelé se musí domluvit, kterou jinou racionální délku použijí. Bez dohody by nejspíš každý zvolil jinou délku, z nekončícího počtu desetinných míst iracionální délky. Naše civilizace předpokládá skutečnost této geometrie a vzniklé matematiky, když uvažuje rozložení hmoty v našem světě. Euklidova geometrie, a k ní příslušná matematika, však jen málo korespondují s vnímaným světem.

Tvor sleduje perspektivní svět, odvozený buďto z Euklidova lineárního prostoru - anebo z diskrétního prostoru. Převod z diskrétního prostoru, do kvadratického kontinua, nevyžaduje iracionální čísla - nezobrazuje nenalezitelnou odmocninu ze dvou, apod. Podle Occamovy břitvy lze snížení počtu druhů čísel, ze dvou na jeden, posuzovat jako výhodu.

Tento odstavec o nelineárním prostoru alternoval Euklidův prostor.

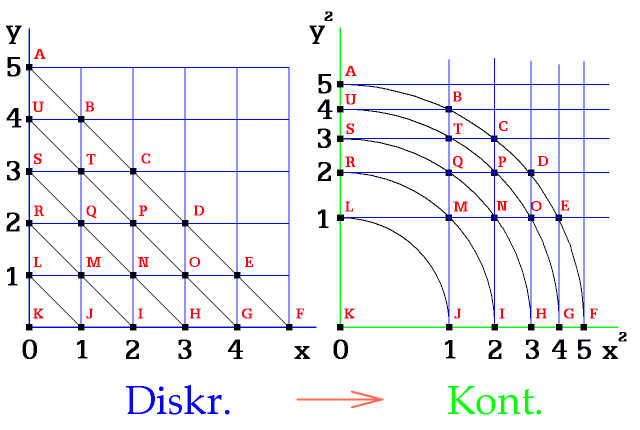
Obr. 7.

Převedení sítě diskrétního prostoru do sítě kvadraticky přepočteného prostoru. Každý bod dodržuje vzdálenost od počátku a i souřadnice svislé a vodorovné osy.

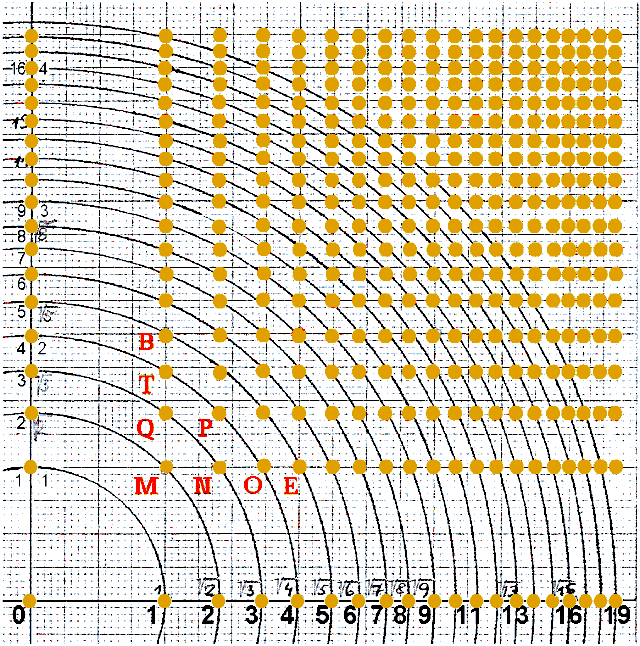
Obr. 8.

Při převodu bodů z diskrétního do perspektivního prostoru se všechny body umísťují na kružnicích s celočíselným poloměrem.

Obr. 9.

Zrak má odvozovat velikost objektu ze zorného úhlu, pod kterým jej pozorovatel vidí. Vlevo jsou vodorovné úsečky, uspořádané pod sebou. Svou délkou vyjadřují velikosti zorných úhlů - v příslušných vzdálenostech od počátku. Znamenají velikost objektů, jak se pozorovateli jeví umístěné v celočíselných vzdálenostech.

Horní pravítko naznačuje, že ve větší vzdálenosti od počátku se úsečky - zorné úhly - zkracují skoro až lineárně. Dolní pravítko ukazuje, že v blízkosti počátku se délky zmenšují nelineárně. Souhlasně s pohledem kamery, která by byla postavená přímo v útvaru pochodujících lidí. Postavy, při své chůzi rovnoměrnou rychlostí směrem ke kameře, se zvětšují zprvu lineárně, ale těsně u kamery vidíme jejich zrychlené zvětšování. To je zde v obrázku připomínáno nelineárním nárůstem délky úseček, blízkých počátku.

ROZPOR:

V kvadratickém prostoru, jejž tato práce sleduje, se liší vzájemná vzdálenost sousedních bodů ležících na společné kružnici. Naopak naše perspektivní vnímání blízkých objektů takovou nerovnoměrnost nemívá. To však nevyvrací názor této práce - důležitost převodu pro zrakový zážitek. Není vyloučen navržený způsob, jak získávat zrakové údaje. K tomu dva důvody:

1. Nejmenší dvě kružnice takový rozpor nemají. Teprve velké kružnice jej mají zdůrazněný. To připomíná zrakový zážitek pozorovatele, jemuž se zmenšují vzdálené objekty, vycházející na obzoru. Viz další práce o Měsíci a Slunci a souhvězdích.

2. Dokonalý obraz, který vnímáme, nemůže biologický orgán, oko, zajistit. Mozek vždy podstatně upravuje zrakové údaje. K tomu práce s mnoha citacemi o práci zraku - hledání virtuální reality.

Obr. 10.

Dosavadní perspektivu nám ukazuje snímek natažených kolejí.

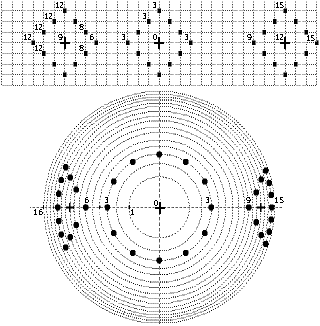
Obr. 11.

Horní obrázek ukazuje čtverce jako kružnice diskrétního prostoru. To proto, že body obvodu mají ke středu svého obrazce (9 či 0 či 12) vždy stejnou vzdálenost - vyjadřováno počtem kroků.

Na dolním obrázku jsou body překreslené do perspektivy středového pozorovatele. Známý poznatek - když pozorovatel vidí opodál kružnici, nakreslenou na podlaze, nevnímá ji ani jako kružnici, ani jako elipsu.

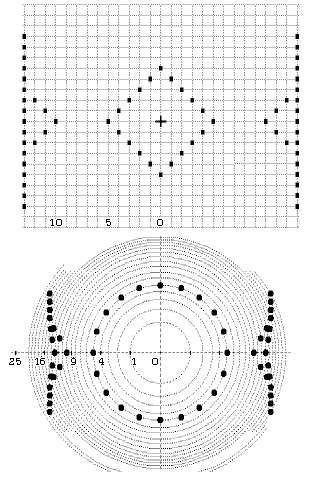
Obr. 12.

Pozorovatel [0] vnímá svislé čáry, jež jsou mu převedené do perspektivy a to z hypotetické vesmírné databáze bodových údajů. Svislé čáry jsou ve středu prohnuté směrem k pozorovateli. Lze snad hledat souvislost s tímto zkreslením svislých čar - viz obrázek HERING ILLUSION (heringbone structure = protisměrné křížové zvrstvení)?

Body z diskrétního prostoru podkládají geometrii perspektivního vnímání. Dodrží jak vzdálenost od počátku, tak souřadnice ortogonálního systému.

Literatura

Nelineární perspektivy - Jindřich Michalik. Bakalářská práce, Univerzita Karlova, Matematicko-fyzikální fakulta, Praha 2012.   (Perspektivy lineární a nelineární - cylindrická a sférická, 52 stran, pdf)