Obr. 2. Dvojrozměrný svět je umístěný v 3D vesmíru - na povrchu koule
Technika dosud využívá jadernou energii a to měněním atomů. Tím prokazuje,
že věda o stavbě atomů ledacos ví - jistě ne všechno. Kdežto názory na
vesmírný prostor takto oprávněné nejsou. Podaří se prokázat podstatu
prostoru nějakým podobně přesvědčujícím způsobem?
Existence elektronů je podložená vlnami, ačkoliv v obalu atomu nemají plynulý spojitý pohyb. Je světový prostor spojitý nebo nespojitý?
OBSAH
Obr. 1. Dvojrozměrné světy - dvě pojetí
Tuto záležitost nepodceňuji, je základem k porozumění vyšším prostorům. Někdy se uvažuje málo domyšlený 2D svět, podle levé části obrázku (obr. 1). Postava se plazí po ploše a užívá směrů vlevo - vpravo či nahoru - dolů. Pardon, není to postava, plazí se. Jenže ona používá i třetího rozměru, protože při svém lezení postupně zakrývá a odkrývá hmotnou podložku, zelenou zem.
Lepší je uvažovat 2D svět podobný světu našemu. Na pravém kruhu se postavy mohou věnovat podobným činnostem - jako my na Zemi. Stavět směrem nahoru. Létat do svého vesmíru. Stačí jim k tomu dva rozměry.
Na levém obrázku je vidět do břicha tvora. Zatímco 2D lékař by musel náročně operovat svého pacienta - otevřel by obvod těla skalpelem, my lidé z 3D objemu vidíme dovnitř 2D těla. Mohli bychom zasáhnout bez rozříznutí těla. Obdobná souvislost je mezi naším 3D a vyšším 4D světem. Tvor ze 4D světa by mohl vstupovat dovnitř naší skříně, aniž by ji otevřel.
««« SLEDOVAT VŠECHNY OBRÁZKY I V LEVÉM SLOUPCI
Obr. 2. Dvojrozměrný svět je umístěný v 3D vesmíru - na povrchu koule
Tyto obrázky spojitého prostoru znázorňují, jak vypadá svět o nižším počtu rozměrů. Otázkou je - jak takový prostor vytvořit pro vnímající vědomí, které dosud žádný prostor nemá? To obrázky nevysvětlují. Kreslíme je na plochu už existujícího prostoru.
Předpokládám, že nelze vložit vědomí do světa, nýbrž představu světa lze vložit do vědomí.
Nabídnu vytvoření prostoru jinak. Podle vzoru předchozích prací II a III vyzkouším tvorbu prostoru způsobem bodového - diskrétního mechanického modelu. I naše sdělovací technika opustila - překonala způsoby analogového signálu a například šelaková i vinylová gramodeska byla nahrazena kódovaným záznamem na kotouči CD. Podobně s televizním vysíláním. Spojitý - analogový signál je překonaný nespojitým digitálním signálem.
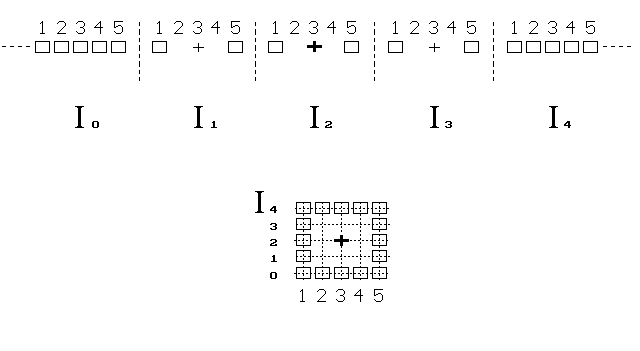
Obr. 3. Vznik nekonečného 1D světa využitím 2D vesmíru
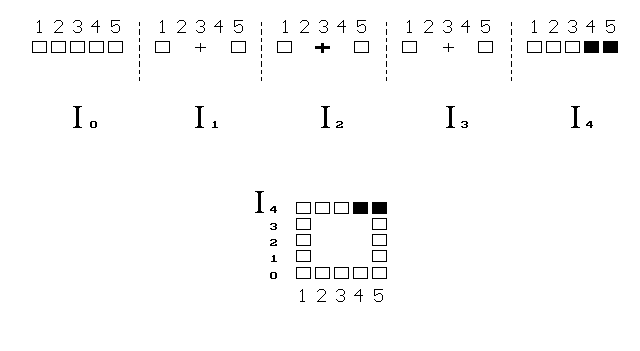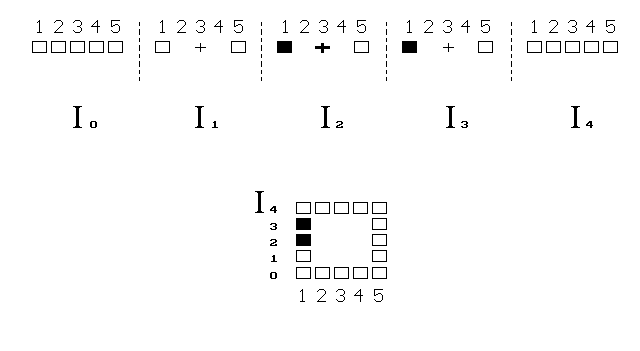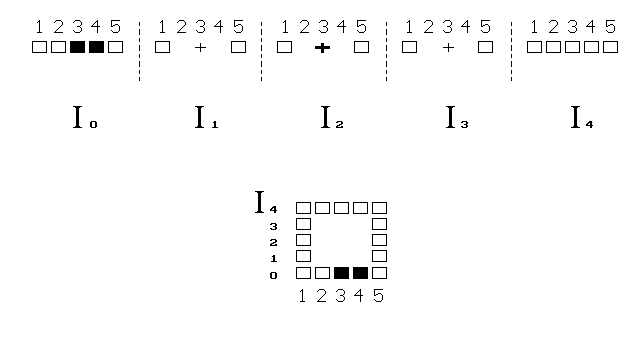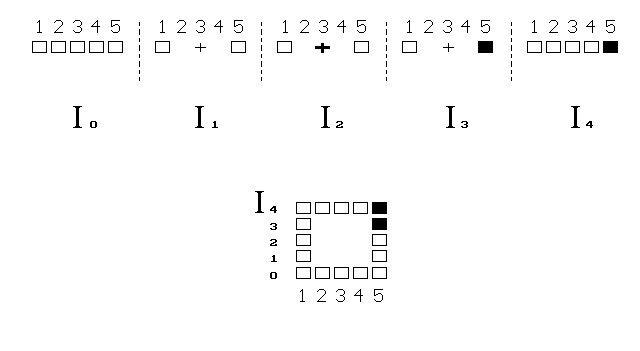
Tvor stěží chápe nakreslené přeskakování svého těla do
dálky, které ukazuje horní část obrázku. A podobně, i my máme potíž
pochopit 4D prostor, zobrazovaný v našem 3D světě obvykle jen na
2D ploše.
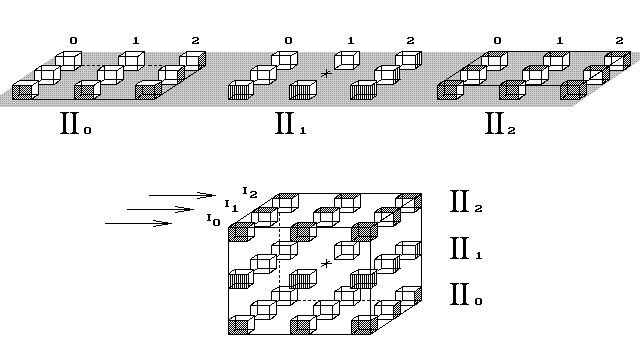
Obr. 5. Dvojrozměrný svět rozložený na vrstvy 3D vesmíru
Nyní chci 2D tvorovi vysvětlit něco o jeho světě. Dole je zobrazen
šikmý pohled na krychli, kdežto nahoře jsou vrstvy krychle
překreslené tak, jak by se objevily na jediné ploše. Přenesl jsem
vrstvy na rovinu. Tvorův svět je ve skutečnosti
obrovský, a do něho zakresluji jen
tři vrstvy II0, II1, II2, vzaté z výukové krychličky o hraně tří bodů.
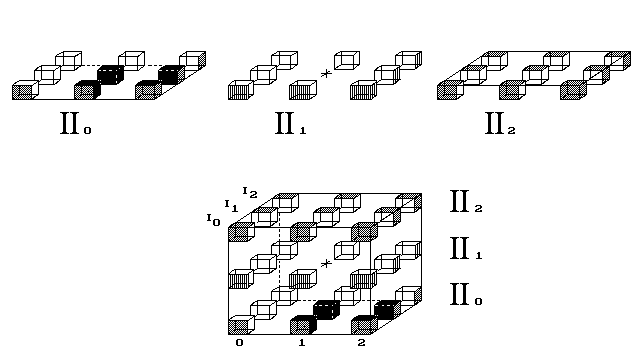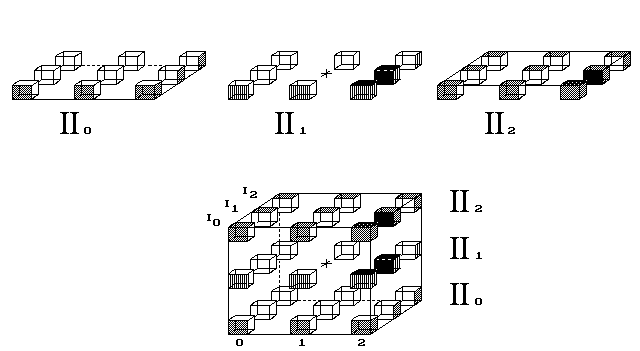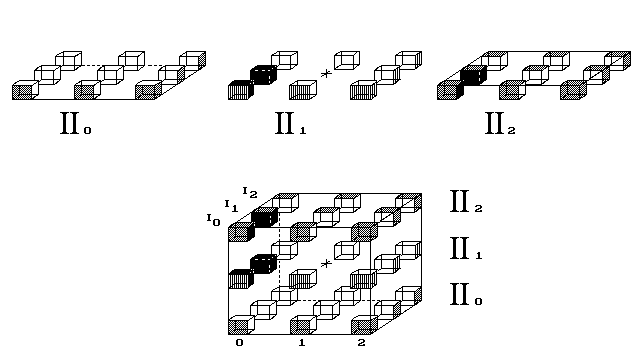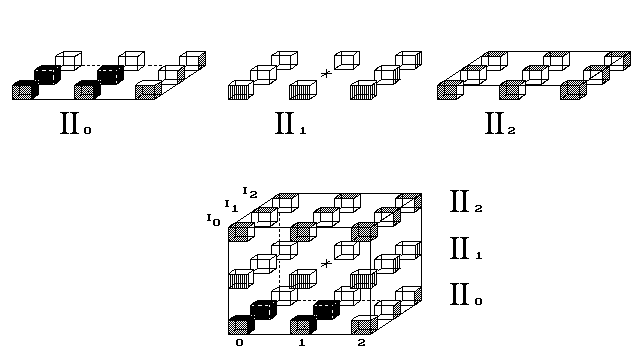
Obr. 6. Čtvereček putuje světem
Vesmír lze navrhnout tak, aby objekt v něm stále putoval
v jednom směru a přitom nikde nenašel okraj vesmíru. K tomu
nestačí nejjednodušší představa vesmíru tvaru koule či krychle.
Podmínku splní 3D svět umístěný na povrchu 4D objektu, například
4D krychle. Povrchem 4D objektu je totiž trojrozměrný prostor.
Vnímáme svět spojitý, svět oblých kružnic. Ten lze odvodit z diskrétního prostoru, viz II. článek. Tvor vnímá přepočtené údaje o bodech hmoty - stlačené perspektivou.
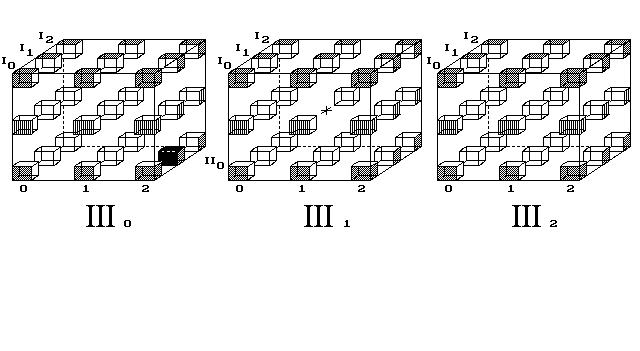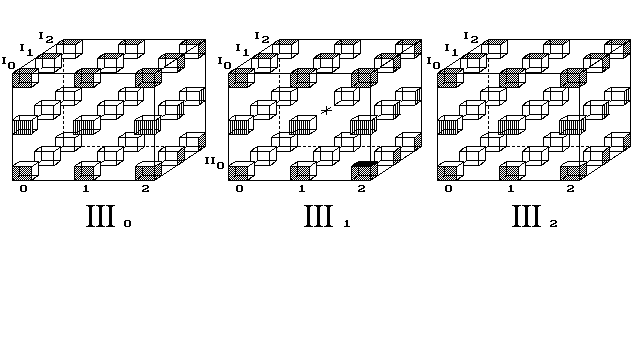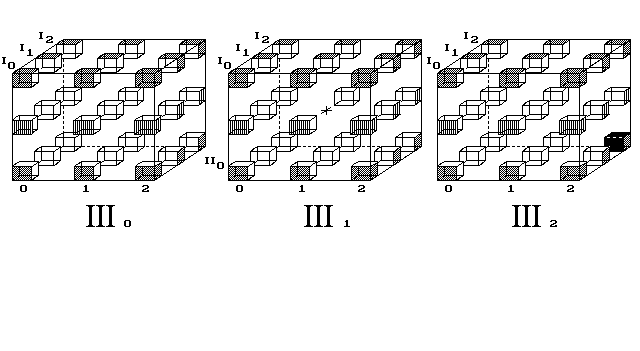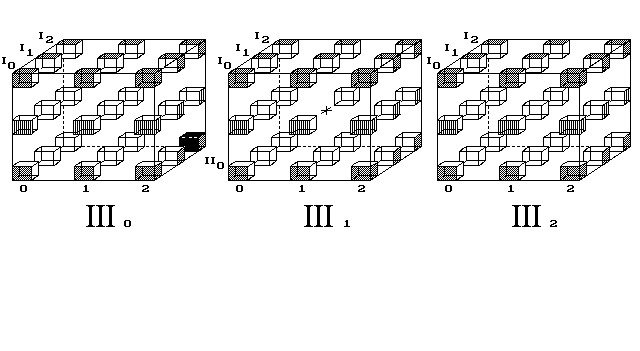
Obr. 7. Bod putuje 3D světem na povrchu 4D vesmíru
Ke vzniku 4D objemu poskládám nyní objemy do řady, podobně jako jsem do řady skládal víc 1D prostorů, které tvořily 2D vesmír v 2. kapitole (obr. 3 a 4). Tam ovšem 1D tvor stěží chápal, že možno přeskakovat z prvního 1D prostoru do sousedního, jaksi do dálky. Podobně v tomto zpodobnění 4D prostoru máme postřehnout, že body přeskakují do sousední posice v sousedním objemu (obr. 7).
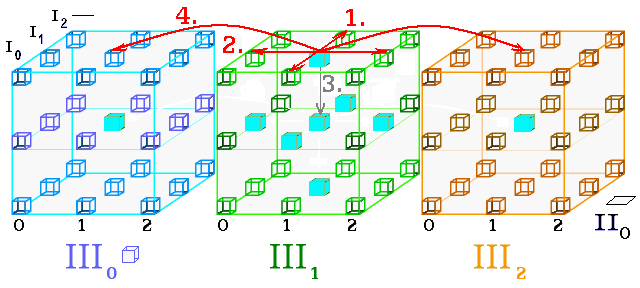
Obr. 8. Body našeho světa ať leží na povrchu 4D krychle. Vevnitř
je barevně odlišný 4D kříž
Při hledání konstrukce světa uvažuji i neznámý čtvrtý směr (obr. 8). Jeden ze čtyř směrů nevyužíváme (3. směr), nesměřujeme dovnitř 3D krychle. Naše hmota je stále na povrchu jedné z krychlí (1. a 2. směr) nebo přeskočí na sousední krychli (4. směr).
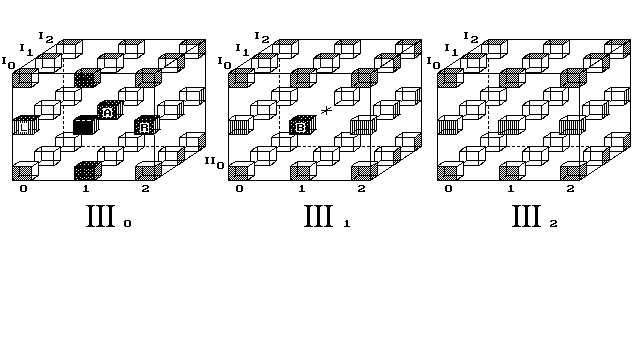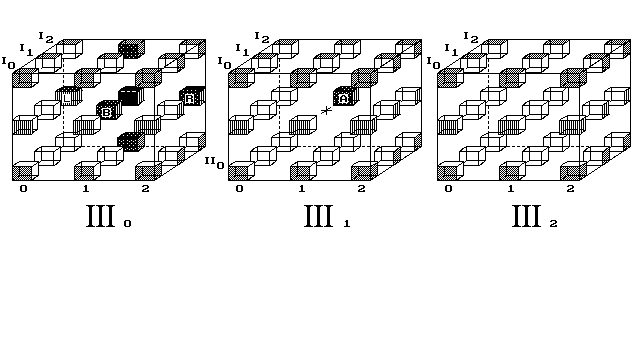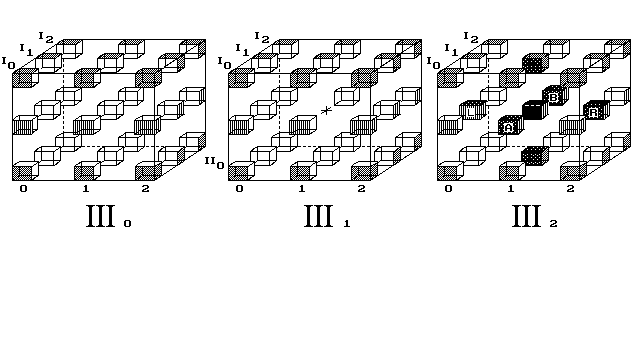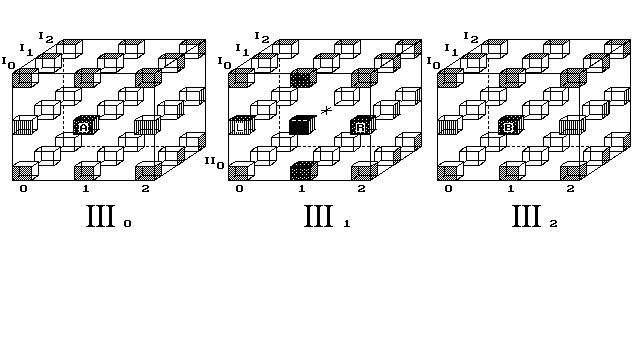
Obr. 9. Objekt tvaru 3D kříže se pohybuje 3D světem
Uskladněné fáze 9. obrázku:Možno studovat i pohyb 3D předmětu v 4D prostoru (obr. 9).
Ukazuji, jak objekt proletí celým vesmírem, vrátí se na místo startu, aniž by změnil směr pohybu.
Pohyboval se po „geodetické kružnici“. Tedy letěl jakoby setrvačností.
Neuplatňoval žádnou sílu pro změnu směru letu. Takový pohyb Vesmírem,
s návratem na místo startu, již dávno uvažovala fyzika -
k tomu zde nabízím i mechanický model.
Nebo lze srozumitelněji ukázat pohyb jednoho bodu „A“ čtyřrozměrným
prostorem po diskrétní geodetické kružnici (obr. 10).
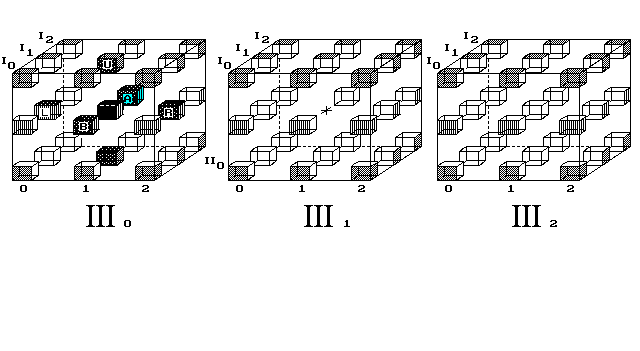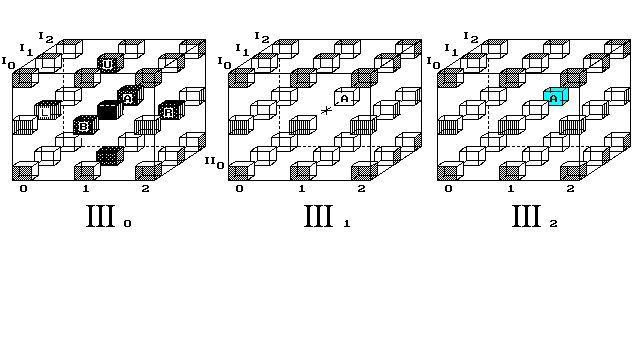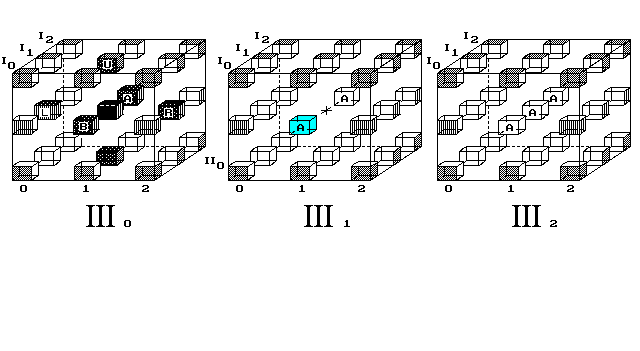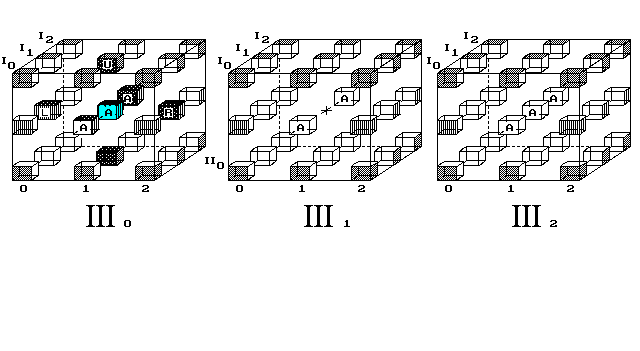
Obr. 10. Bod se po průletu celým vesmírem vrátí na místo startu
4D vesmír kreslím jako dutou 4D krychli, do jejíhož vnitřku se nedostáváme. Proč čtyřrozměrnému vesmíru, o hraně 3 body, kreslím vnitřní krychli jako dutou a obě krajní jako plné? Je to v souladu s chápáním obyčejné 3D duté krychle. Ta, v bodovém provedení, má všechny své vrstvy - čtverce duté, pouze horní a dolní čtverec, tedy základny krychle, jsou plné.
A zde, v 4D krychli, obdobně musí být krajní krychle zaplněné body a vnitřní krychle duté. Pohyb bodů světem neuvažuji v posicích, ve kterých nejsou nakreslené body. Zde se to týká jen jediné, vnitřní posice [III1/II1/I1/1] střední krychle.
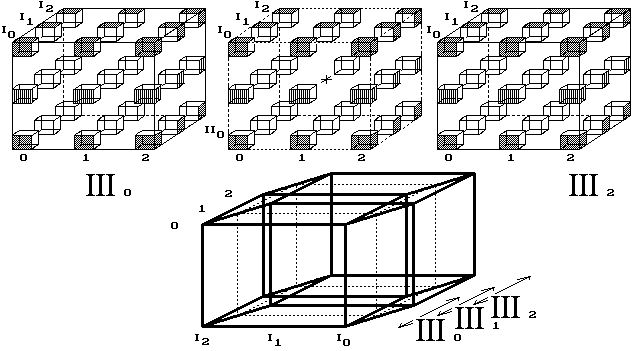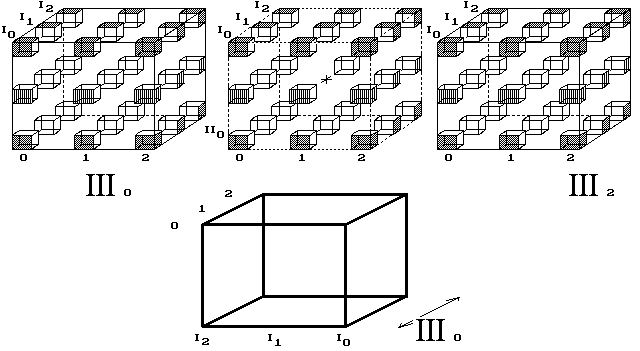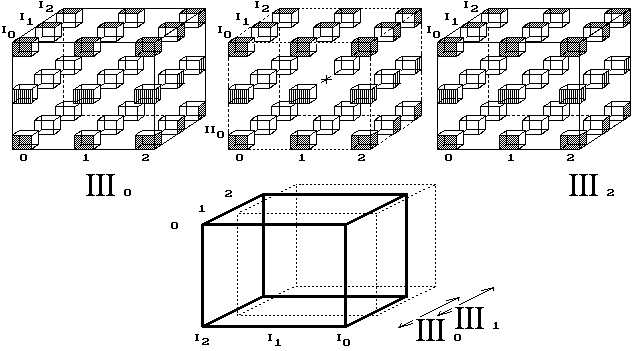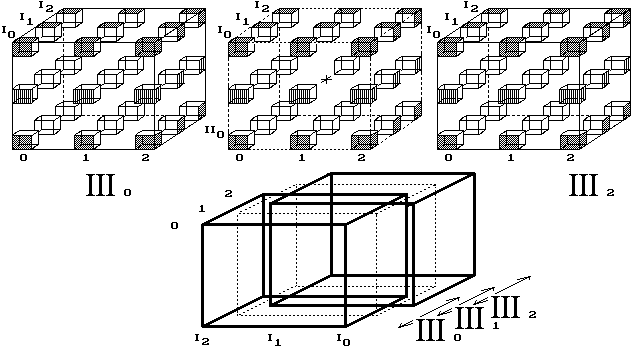
Obr. 11. Vznik 4D krychle
Takže my chápejme, že 4D prostor vzniká z diskrétních objemů, které se jen jakoby prostupují, posunuté vždy o jednu posici. Je potřeba 4. směru, ve kterém se umísťují objemy, aniž by se vzájemně prostupovaly. Čtyřrozměrnou krychli, o hraně délky tři body, tvoří tři trojrozměrné krychle. Tvor by vnímal čtyři kolmice, všechny čtyři směry k sobě vzájemně kolmé. Nemožné? Dokud nevíme, jak se konstruuje náš vesmírný prostor, pak nesuďme. Určující je k tomu počet sousedních posic.
Spojitý prostor, který vnímáme zrakem, vysvětluji jako kvadraticky přepočítaný z diskrétního prostoru (viz III. článek). Na třech pravoúhlých osách nejsou souřadnice rozložené lineárně, ale kvadraticky. Ne x, y, z, ale x2, y2, z2.
Problematika je snáze přijatelná, když přijmeme hmotný svět jako záležitost nadřazené Informatiky.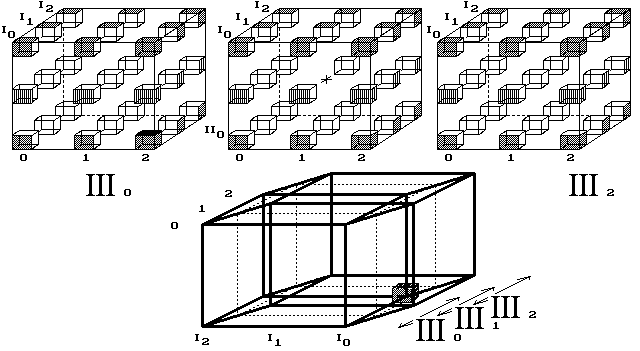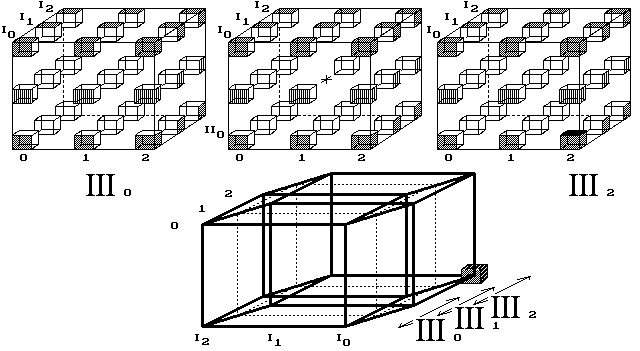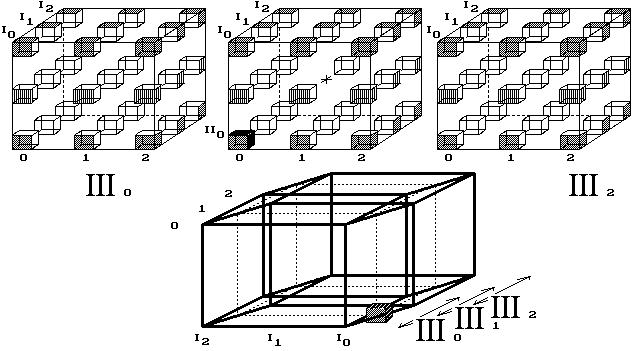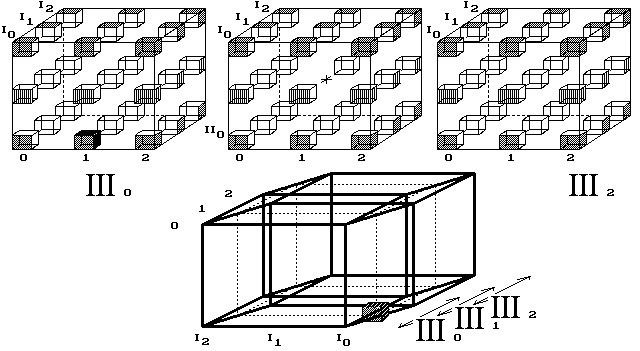
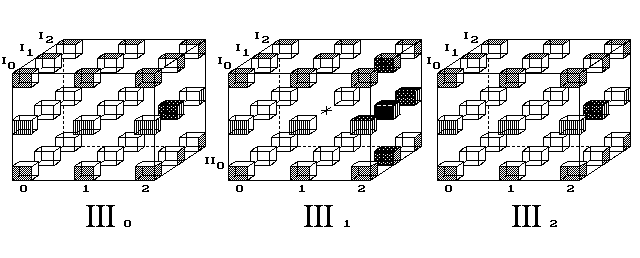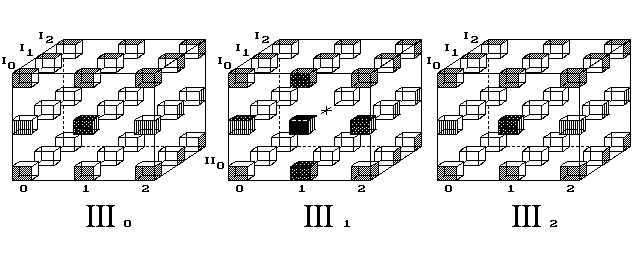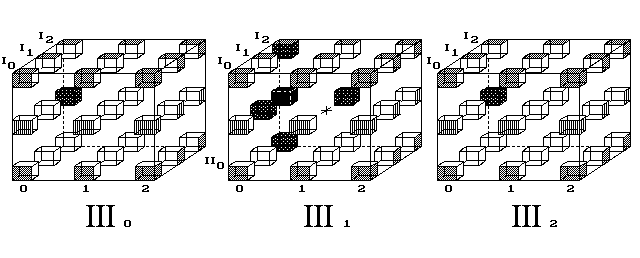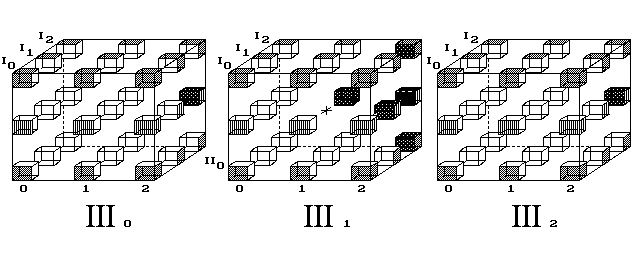
Obr. 12. Bod obíhá po čtverci. Po přepočtu do perspektivního
prostoru by pozorovatel sledoval oběhy po kružnici; pokud by byl
v jejím středu nebo nad ním
Zajímavá je následující situace (obr. 12). Nahoře, na třech samostatných krychlích,
pohyb bodu nepřipomíná, že by se pohyboval po ploše. Vždyť
přeskakuje v trase přímky. Ale dole, na průmětu 4D prostoru na plochu,
je vidět, že trasa bodu vede plochou, nikoliv přímkou.
Obr. 13. Trojrozměrný kříž proletí celým vesmírem
Obr. 14. Jděte na 15. obrázek
Krychlička letí jen částí vesmíru (obr. 14, 15).
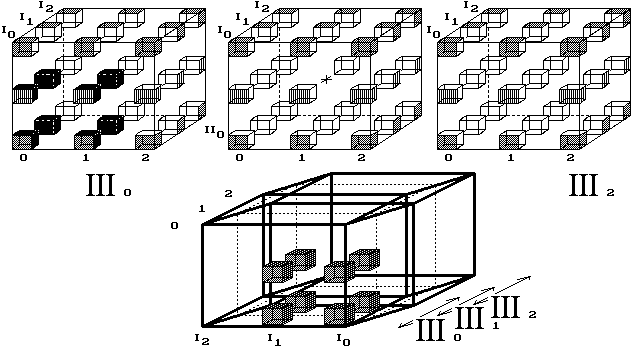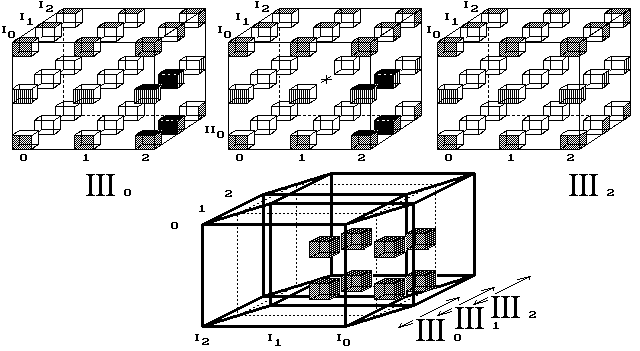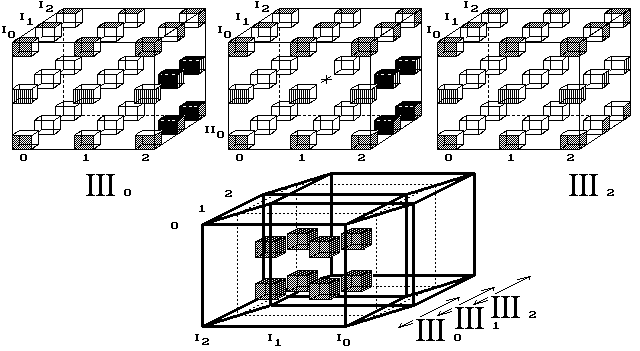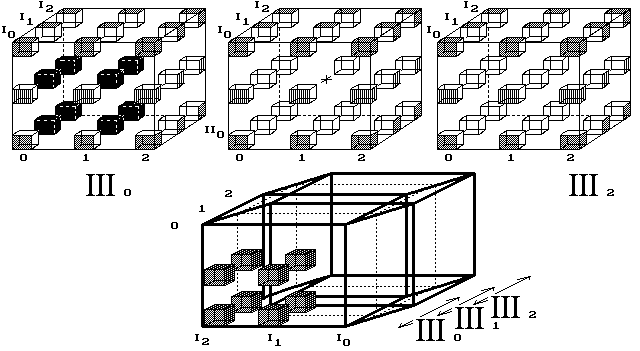
Obr. 15. Těleso neproletí celým vesmírem
Svět s n rozměry lze umístit na povrch vesmíru s (n+1)
rozměry. Body diskrétního prostoru lze pak přepočítat ve prospěch
spojitého perspektivního vnímání tvora.
Trojrozměrný předmět může letět světem do stále další sousední
posice, aniž by na něj působila síla. Letí přímo a to setrvačností.
Přesto se vrátí na původní místo svého startu.
Čtverec diskrétního prostoru lze přepočítat do spojitého perspektivního prostoru. K tomu je nutné čtverec, kreslený v pravoúhlých souřadnicích, postavit na jeho vrchol. Podobně krychle, zobrazené zde v obrázcích, lze uvažovat jako postavené na rohu. Nebo užít ve prospěch 4D prostoru, namísto krychle - šestistěnu, raději osmistěn?
Užité zjednodušení usnadnilo sledování bodových obrázků.