
Immanuel Kant

Obr. 1.
Neeuklidovské prostory

Obr. 2.
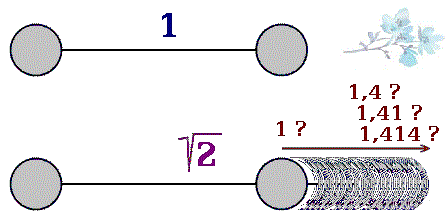
Geometrická vzdálenost mezi
protějšími vrcholy čtverce je konečná
a přesto je její výpočet bez konce!
Iracionální výsledek neposlouží, nýbrž řešitel si vybere některé
racionální číslo jako nepřesný výsledek.
Dvě úsečky se liší výhradně kvantitativně, kdežto kvalitu mají jedinou - proč tedy dva druhy čísel?
Obr. 3.
Pokračujícím výpočtem se počítaná délka stále jen upřesňuje, například prodlužuje. Výsledek nevznikne!
Obr. 4.
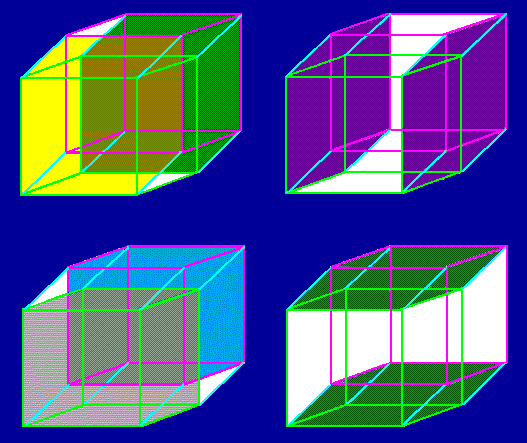
Svými smysly ve světě nezjišťujeme nejen čtyřrozměrné krychle, ale ani 3D objekty nevidíme v Euklidově prostoru. Lineární spojitý prostor je hypotézou.
Obr. 5.
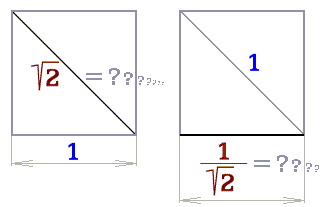
Nesouměřitelnost. Po výpočtu
Pythagorovou větou se někdy udává vzdálenost jako racionální,
jindy iracionální, aniž by se na ostatních fyzikálních
vlastnostech bodů nebo vzdálenosti v prostoru něco změnilo.
Obr.6.
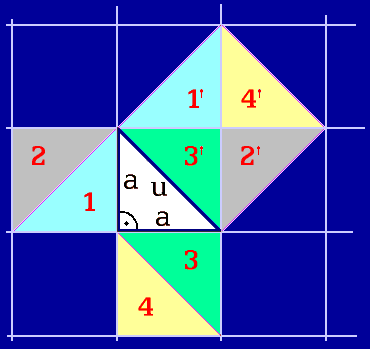
Jenže pohledem zjišťujeme obrazec
podrobený perspektivě.
Obr. 7. Různoběžky či rovnoběžky (podle www.gymfry.cz)
Názor Ernsta Macha: zvláště fyzika získá největších
vysvětlení od biologie, a to analýzou smyslových počitků.
Filosof Karl Raimund Popper: předpokladem vědeckého pokroku je
vyvratitelnost přijímaných poznatků.