„Když uděláte ze čtverce kruh, pak naleznete vše tajné“
* * *

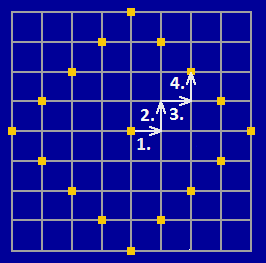
Obr. 1. Kružnice diskrétního prostoru. Každý z bodů obvodu má ke středu stejnou vzdálenost
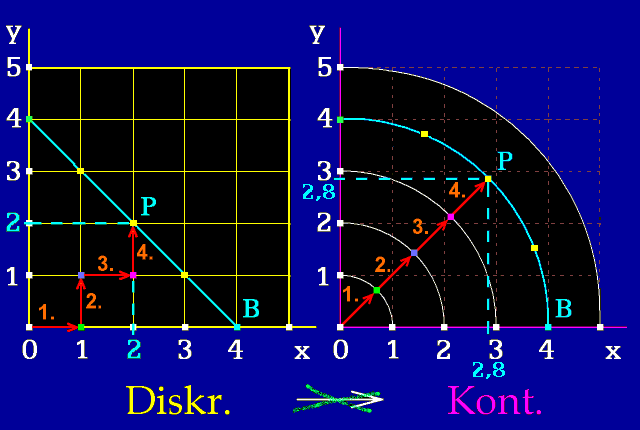
Obr. 2. Převod bodů z diskrétního do Euklidova prostoru nemá řešení

Obr. 3. Je snad řešitelný převod bodů z diskrétního do perspektivního prostoru?
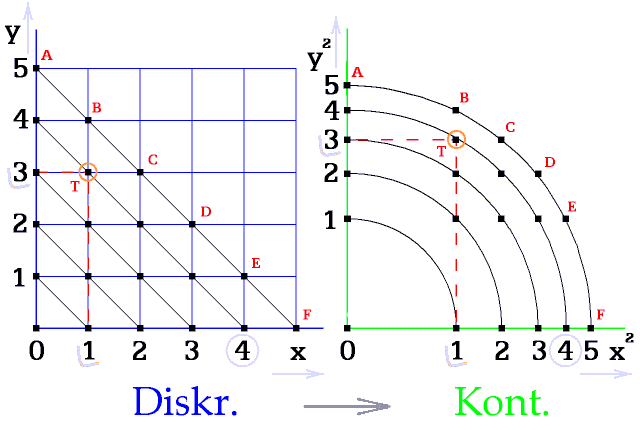
Obr. 4. Každému bodu, převedenému z diskrétního do perspektivního prostoru, zůstává stejná vzdálenost od počátku (4) a také obě souřadnice [1, 3]
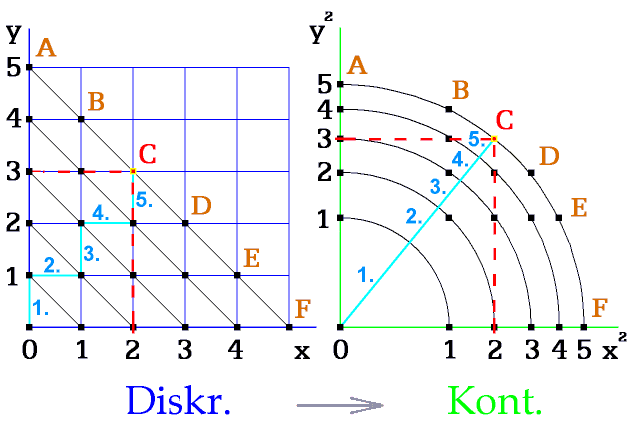
Obr. 5. Vzdálenost vyznačená kroky
Chod Vesmíru ať se odehrává v diskrétním prostředí. Z něho tvor dostává údaje přepočítané do zrakového vnímání.Tvor je vždy umístěný v počátku souřadnic, odkud vnímá prostor perspektivně rozložený.
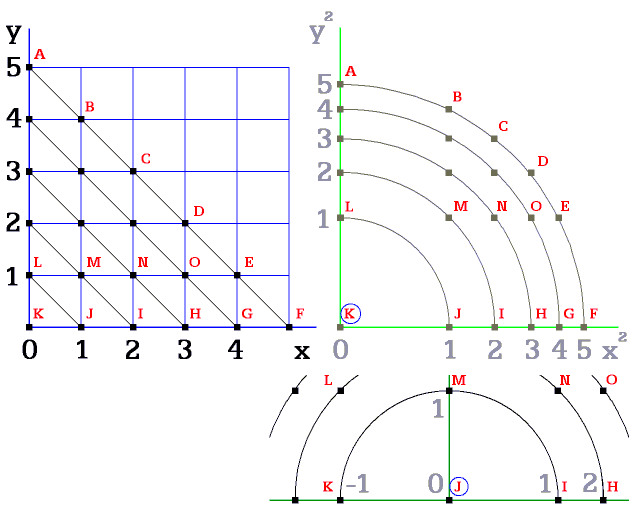
Obr. 6. Každý pozorovatel je středem svého systému
Tvor vždy zjišťuje svůj první krok o stejné délce. Z toho získává dřevní názor, že celý svět je lineární.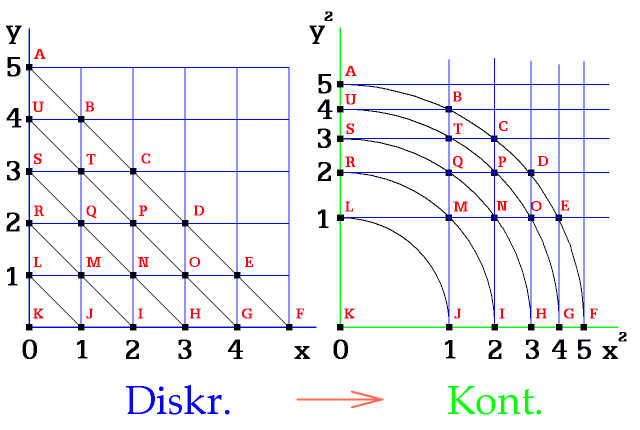
Obr. 7. Prostory vyznačené sítí
Každý bod dodržuje vzdálenost od počátku a souřadnice svislé a vodorovné osy.
Obr. 8. Přepočítané body leží na soustředných kružnicích
Při převodu bodů z diskrétního do perspektivního prostoru se všechny body umísťují na kružnicích s celočíselným poloměrem.

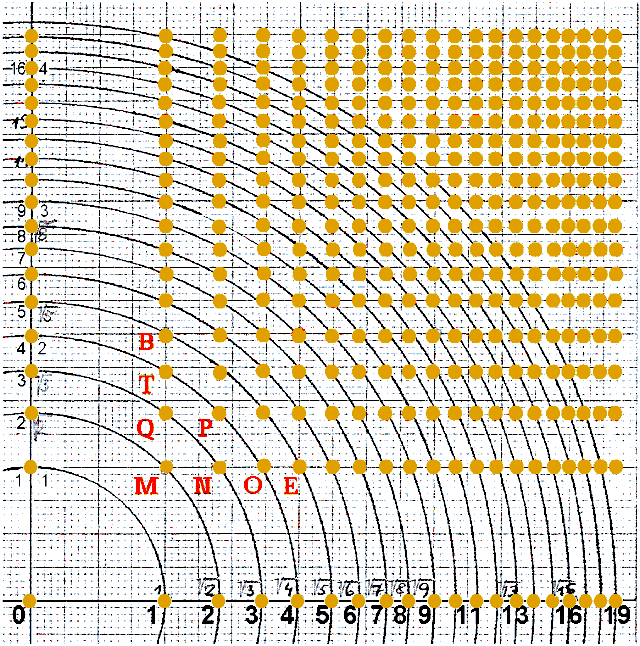
Obr. 9. Nelineární nárůst délky pro vodorovné úsečky, blízké počátku
Zkušenost v filmového záznamu. Postavy, při své chůzi rovnoměrnou rychlostí směrem ke kameře, se zvětšují zprvu lineárně, ale těsně u kamery vidíme jejich zrychlené zvětšování.
Obr. 10 Perspektiva
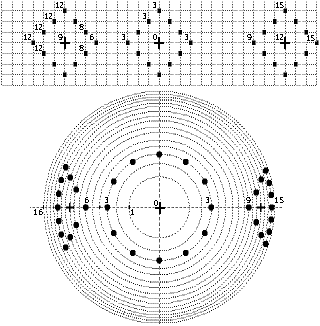
Obr. 11. Čtverce - kružnice diskrétního prostoru
Když pozorovatel vidí opodál kružnici, nakreslenou na podlaze,
nevnímá ji ani jako kružnici, ani jako elipsu. Projeví se
perspektivní zkreslení.
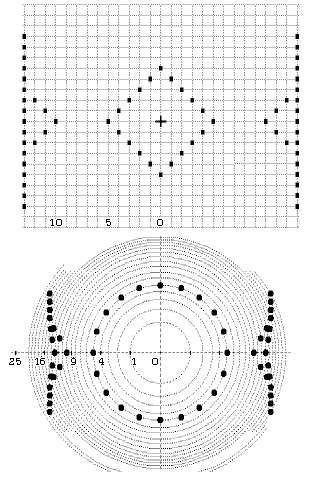
Obr. 12 Převod čar pozorovateli v počátku [0]
Připravil
B. T.
Interakce prostorů