Využití čtyřrozměrného prostoru

Červí díry - VIII   💾

verze 5. 2017a

Bohumír Tichánek

*   *   *

Mechanický model astronomické červí díry stěží vymyslíme ve spojitém Euklidově prostoru. Riemann uvažoval náš svět umístěný na povrchu 4D tělesa, ve 4D prostoru. Takové těleso má 3D povrch. Lze hledat kratší trasu vevnitř 4D tělesa, jež spojí dvě vzdálená místa Vesmíru. Tímto směrem zde řeším mechanické modely diskrétního prostoru.


*   *   *

OBSAH

  1. Úvod
  2. Řešení v diskrétním 4D prostoru
  3. Cestu zpět v čase řešil Jules Verne
  4. Krátce z diskrétního časoprostoru
  5. Závěrečná nesnáz
    Literatura
*   *   *

1. Úvod

Fyzika, řadu let, zná pojem červí díry. Je to spojení - zkratka mezi dvěma oblastmi časoprostoru. Předložil ji k diskusi poprvé John Wheeler.

„Jsou řešením Einsteinových rovnic a spojují jinak vzdálené části jednoho vesmíru, nebo dokonce místa v jinak oddělených vesmírech.“ [1]

„Červí díra se někdy označuje jako Einstein-Rosenův most. Astronaut se může z A do B dostat červí dírou rychleji, než to dokáže světlo. A díky tomu, že takto světlo předběhne, může cestovat i zpátky v čase.“ [2]

Červí díra je tedy zvláštní tunel ke spojení dvou vzdálených oblastí časoprostoru. Získala označení podle červa, který nepoleze po povrchu jablka, nýbrž ví, jak použít zkratku, ve které se onehdy zadarmo najedl (obr. 1). Prokousal si střed jablka a tím získal červí díru. Prosím, přesně takoví červi nebývají, ale podobně málo víme o výskytu fyzikálních červích děr ve Vesmíru. Pouze nevědecké poznatky o UFO tvrdí, že tyto „létající talíře“ cestují rychle využitím „nadprostoru“. Nesrovnatelně rychleji, než letí světlo. Červí díra zkouší obhajovat takové možnosti.

Obr. 1.  Zeleným jablkem vede červí díra, která poskytne červovi kratší trasu než po povrchučerví díra - jablka ve fyzice

Obyčejný tunel spojuje dvě místa v prostoru. Kdežto červí díra spojuje dvě místa v časoprostoru. Umožňuje dostihnout vzdálené místo dřív než světlo; to fyzika nazve překonáním času.

Vzdálenost středem jablka měří dvakrát poloměr. Vzdálenost po povrchu půlky jablka je přibližně třikrát poloměr; používá Ludolfovo číslo. Výpočet obvodu kružnice v Euklidově prostoru je vždy nepřesný, lze užít například π = 3.


2. Řešení v diskrétním 4D prostoru

Hypotetickým červím děrám sleduji řešení v trojrozměrném diskrétním (bodovém) prostoru, který se nachází na povrchu 4D krychle (6obr16). Takovou myšlenku Vesmíru se čtyřmi délkovými rozměry, ze kterých známe jen tři, zavedl Bernhard Riemann (1826 - 1866).

Na diskrétním obrázku vede obyčejná dlouhá cesta po povrchu 4D krychle; má délku čtyř kroků (obr. 2, obr. 4). Je to ovšem jen zkrácení cesty geometrickým prostorem, nezavádí časoprostor.

Tato diskrétní řešení lze převést do geometrie zrakových zážitků našeho 3D spojitého světa. Je-li pozorovatel umístěný ve středu objektu, pak mu lze čtverec (postavený na vrchol) přepočítat v kružnici a krychli zase v kouli perspektivního prostoru. Podobně se 4D koulí.

Bod se sune povrchem diskrétní krychle

Obr. 2. Vesmír jako 4D krychle o hraně, která čítá 3 posice. Po 4 krocích je bod v cíli.

Náš svět má tři směry, a stejně na tom je povrch 4D krychle. To nabízí přijmout povrch 4D tělesa jako náš svět. A především - vzniká 3D svět bez okrajů, podobně jako i 2D povrch naší Zeměkoule nemá okraje.

Bod se sune červí dírou


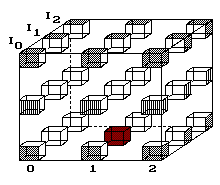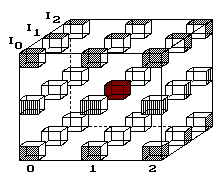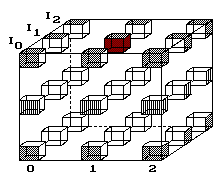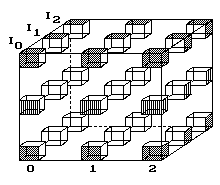
Obr. 3. Bod se přesunuje červí dírou. V cíli je už po 2 krocích.

Když se bod sune vnitřním objemem krychle, pak mu stačí 2 kroky (obr. 3). Po povrchu by to bylo víc, 4 kroky.

Lze spekulovat o jiných zákonech pro pohyb v zakázaném prostoru. Vnitřními posicemi 4D krychle ať lze cestovat bez omezení světelnou rychlostí.

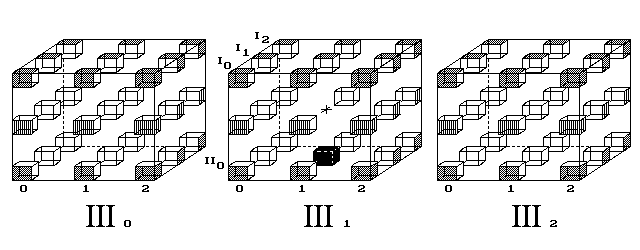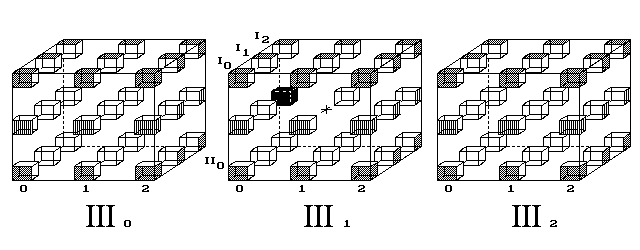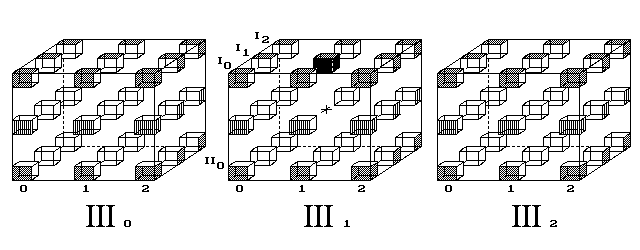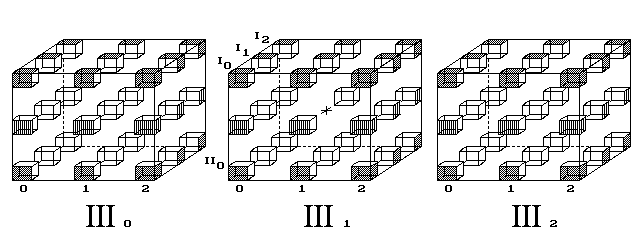
Trojrozměrný svět nenalézá mechanický model k vysvětlení červí díry. Kdežto povrch 4D tělesa jej přibližuje. Čtyřrozměrný diskrétní prostor posuzuji jako databázi, jež podkládá naše vnímání spojitého světa.

Nechť hrana 4D krychle čítá 3 body. Pak ji tvoří 3 krychle (obr. 4). Posice vevnitř objemu III1 je zakázaná, slouží hypotetické červí díře. Všechny ostatní posice objemů III0, III1 a III2 jsou povrchem 4D krychle.

Je-li geometrie Vesmíru tvořena diskrétní 4D krychlí, pak je sousedních 3D krychlí obrovské množství s ještě větším počtem vnitřních zakázaných posic.


Pohyb bodu v 4D objemu

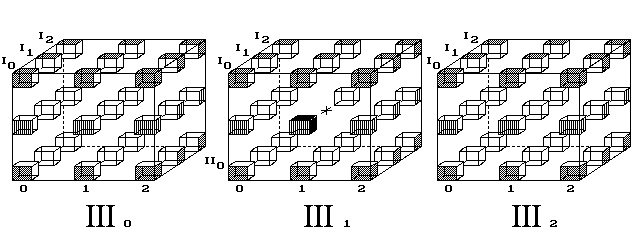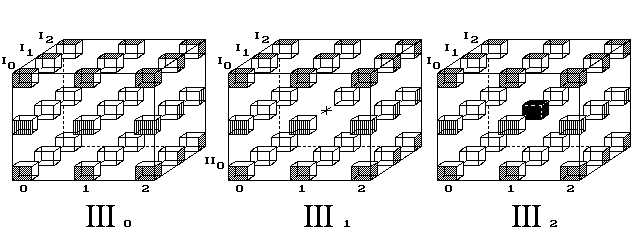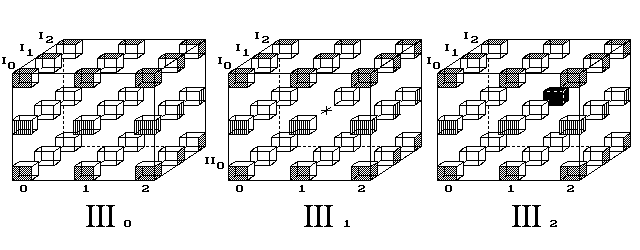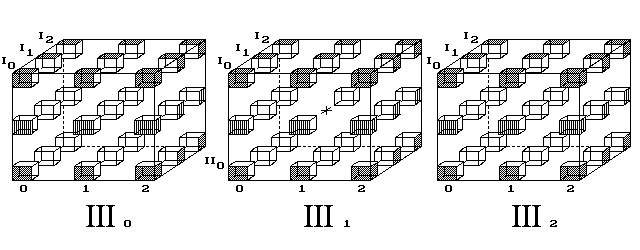
Obr. 4. Cesta nemusí vést jediným ze tří objemů 4D krychle, jak ukazoval 2. obrázek. Trasa stejné délky 4 kroků vede tentokrát přes sousední objemy


3. Cestu zpět v čase řešil Jules Verne

V mém modelu to s cestováním zpátky v čase nebude tak žhavé, jak jsem v úvodu citoval [2]. Srovnám cestování v čase nazpět při pohybu po Zeměkouli (3.1.) a skrz červí díru (3.2.).

3.1.

Na Zemi můžeme cestovat zpátky v čase. Ve střední Evropě mějme 13 hodin a v Americe ať je teprve 8 ráno. Takže záleží na rychlosti letu, kterou se cestovatel dostane od nás do Ameriky a ačkoliv u nás již poobědval, může tam za pár hodin poobědvat znovu - pokud přeletěl velkou rychlostí. Vrátil se v čase, ale nikoliv do místa startu.

Jules Verne, na vrácení času zpět, založil důležitou finální zápletku v románu "Cesta kolem světa za 80 dní". Cestovatel získal celý 1 den a přitom se vrátil do místa startu!

Ve skutečnosti je to jen legrační paradox. Cestou do Ameriky se nevracíme v čase, ale v označení času (data). Zajisté necouváme do svých minulých dějů.

3.2.

Jednodušeji se to jeví s průletem touto červí dírou. Kosmonaut - červonaut by mohl předběhnout světlo v čase, protože zná zkratku. Vynoří se na jiném místě, kde tamním lidem radiové vlny dosud nedoručily zprávu, kterou červonaut přináší. Ale nevrátí se do minulosti v místě svého startu.

Zdánlivě by vyvinul nadsvětelnou rychlost, ale když by pak prozradil svou trasu (obr. 3), nemusel by se nikdo v hrobě otáčet.


4. Krátce z diskrétního časoprostoru

Minkowského diagram vysvětluje, že objekty se pohybují časoprostorem (obr. 5). Jsou-li bez pohybu, pak stoupají po časové ose. Jinak je jejich čára šikmá, až po dráhu světla pod úhlem 45 °.


Minkowského diagram dynamicky

Obr. 5. Minkowského diagram

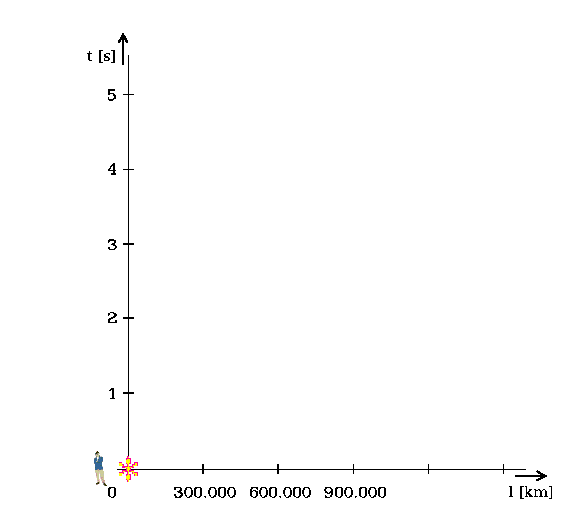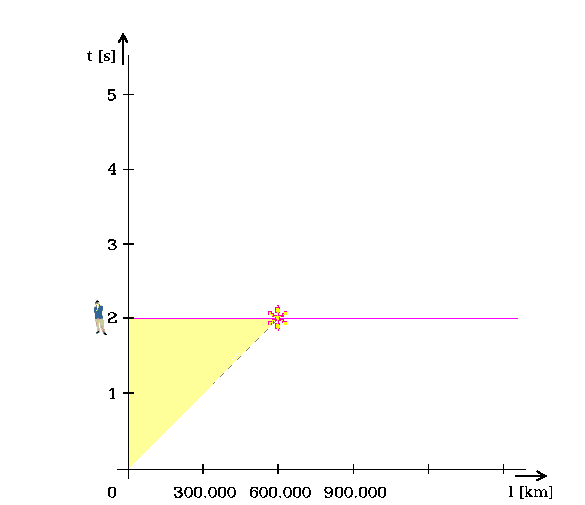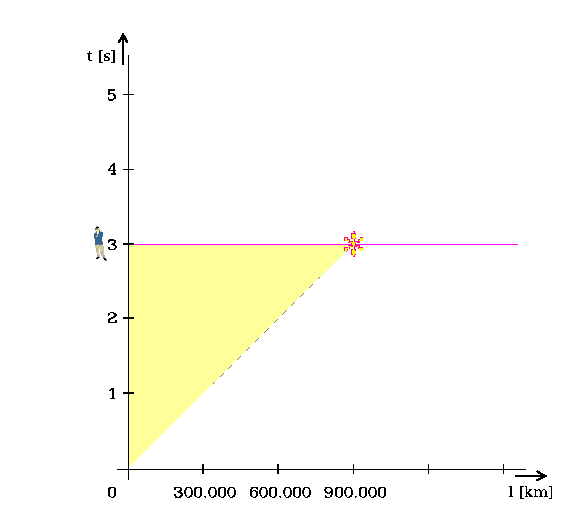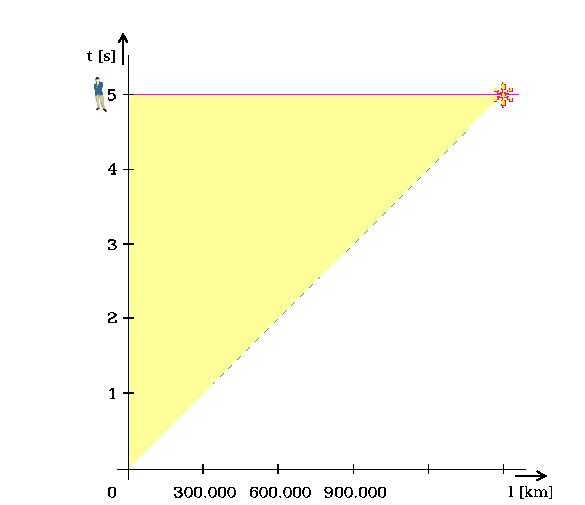
Ve své práci o diskrétním časoprostoru zdůvodňuji zpomalování času při pohybu. Namísto Minkowského diagramu užívám souměrný časoprostor. Čas nanáším na svislou a dráhu na vodorovnou osu. Přepočet z diskrétních pulsů do spojitých veličin řeším převodem do perspektivy (obr. 6). Perspektivní osy jsou časová tq a délková lq.

Časoprostor v Euklidově a v perspektivním prostoru

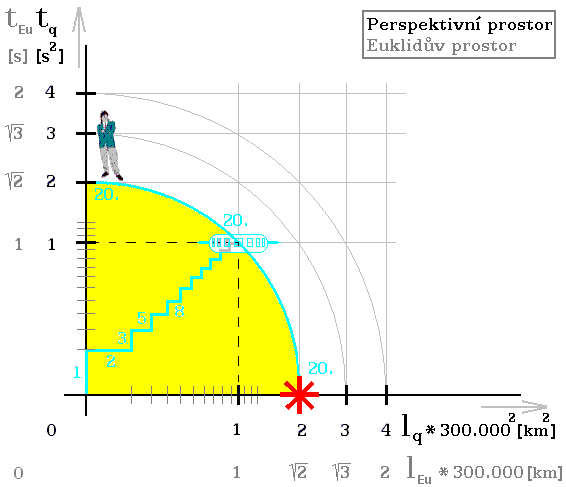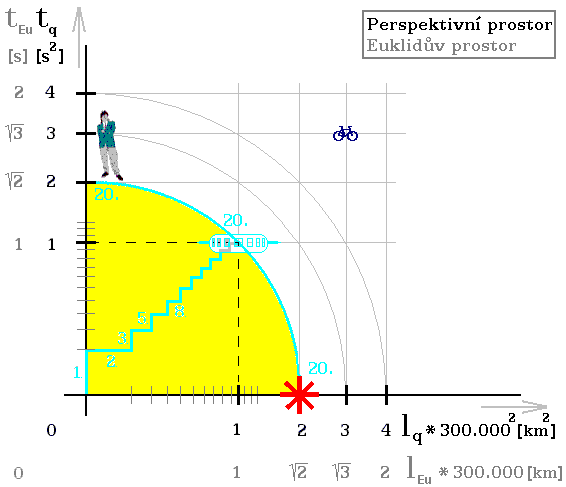
Obr. 6. Objekt předstihl obvod rostoucí čtvrtkružnice, protože prošel červí dírou

Červí díra dovoluje, aby objekt předstihl růst kružnice, viz jeho umístění v [3, 3].


5. Závěrečná nesnáz

Uvažovat náš svět, jednoduše rozložený na povrchu diskrétní 4D krychle, má nevýhody. Roh krychle má jen tři sousední posice, cesta přes něj vyžaduje víc kroků než mimo roh. Šikmé kroky nezavádím; tudíž cesta bodu užívající hrany krychle, by byla delší - červená trasa (obr. 7). Následně sleduji jiné uspořádání 4D diskrétního prostoru na povrchu 4D krychle. Zkoušel jsem posoudit i jiné 4D útvary.

Diskrétní 4D prostor žádá pravoúhlé kroky


Obr. 7. Šikmé kroky nejsou dovolené, červená trasa ukazuje 6 nutně pravoúhlých kroků

*   *   *
Zajisté celá problematika je složitější než jednoduchý model. Zde jsem sledoval možnost, jak zkrátit cestu prostorem. Předpokladem je využít hypotetický čtvrtý geometrický rozměr prostoru. Znalosti stavby Vesmíru jsou dosud nehluboké. Názory na spojitost a na iracionální velikosti veličin v našem světě podkládáme především smyslovým poznáním, posouzeným jen do určité hloubky.


      Literatura

[1] Šíp času - Peter Coveney, Roger Highfield. Oldag, Ostrava 1995, s. 119, s. 434
[2] O čase. Einsteinova nedokončená revoluce - Paul Davies. Motýl, Bratislava 1999, s. 308


    Poznámka


Využití těchto diskrétních modelů n-rozměrných prostorů, pro zobrazení červí díry, pochopil (již odešlý) Ing. Souček z České astronomické společnosti, sekce kosmologické. Upozornil na toto využití, před delší dobou - při výročním setkání.