Sestrojení vícerozměrného prostoru lze studovat v diskrétním - bodovém prostředí. Z diskrétního prostředí lze posice bodů přepočítat do spojitého prostoru, který má perspektivně stlačené cejchování os.
Prostory s vyšším počtem rozměrů posuzuji jako sestavu, která je
odvozená z méněrozměrných prostorů. V diskrétním prostředí je to
samozřejmým postupem. Kdežto spojitému prostoru není známý způsob jeho
konstrukce, například pro trojrozměrný (3D) prostor. Vždyť i v
zastaralé záznamové technice spoléhal analogový, tedy spojitý obrazový
zápis, na zapamatování v oddělených molekulách látky, diskrétně.
V objemovém 3D prostoru lze zrcadlově otočit dvojrozměrný objekt - písmeno L - tak, že po otočení připomíná písmeno J. Kdežto žádným otáčením na 2D ploše písmeno L nelze takto otočit.
Podobně se usuzuje, že lze otočit 3D objekt ve 4D prostoru. Takže například pravá bota se vrátí otočená a je z ní bota levá. Což pro nás zní jako pohádka.
Abychom využili diskrétního prostoru pro posouzení takového úkolu, nejprve si osvojme postupy v 2D a 3D prostoru.
Nejkratší úsečka, složená ze dvou bodů, se otáčí v 2D prostoru (obr.
1). Přitom jednomu bodu nějaké otáčení v posici neuvažujme;
nesledujme chování osy otáčení. To proto, že bod
je informací 1 bitu o obsazení posice a další
informace, o jeho pootočení, se nevyskytuje.
Obr. 1. Otáčení úsečky délky 2 body
V 1D prostoru - na přímce - by se úsečka točit nemohla. K otočení by bylo potřeba, aby body přeskakovaly až do některé vzdálené posice. Zde však zaveďme přeskoky vždy jen do sousední posice. Pokud ovšem byl svět předem projektovaný, zkonstruovaný a nyní je provozovaný, pak je možné předpokládat ledacos dalšího - ostatně jak jinak, když v něm platí zákony. V zavedených přístupech ať bod přeskakuje vždy jen do sousední nachystané posice. Při pohybu postupně navštěvuje místa tak málo vzdálená, až následně uvěříme ve spojitý prostor.
Přeskakující bod míří vždy do své sousední posice. Šikmé kroky povolené nejsou, takže vzdálenost přeskakujícího bodu vůči počátku [I0/6] se stále mění - činí 1 krok, pak 2 kroky a zase znovu.Nyní otáčení delší úsečky vytvořené čtyřmi body (obr. 2.). Jejich přeskoky předepšme tak, aby se co nejméně odchýlily od představy otáčení úsečky ve spojitém prostoru.
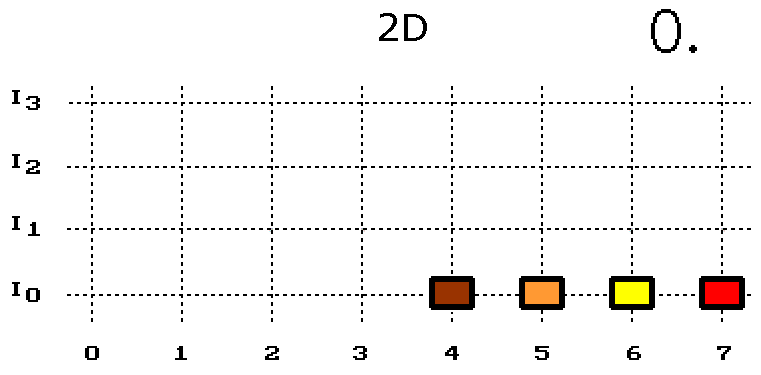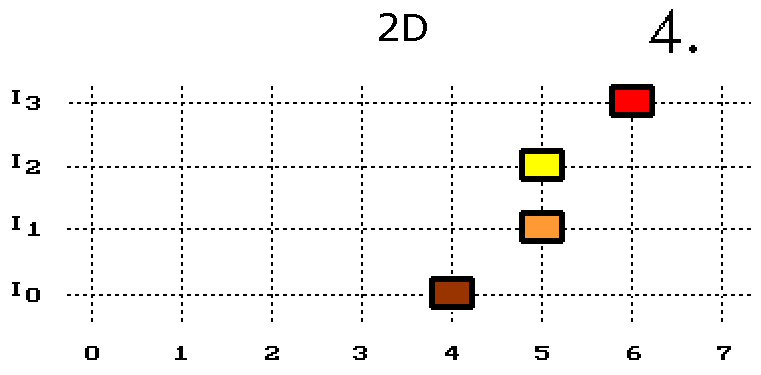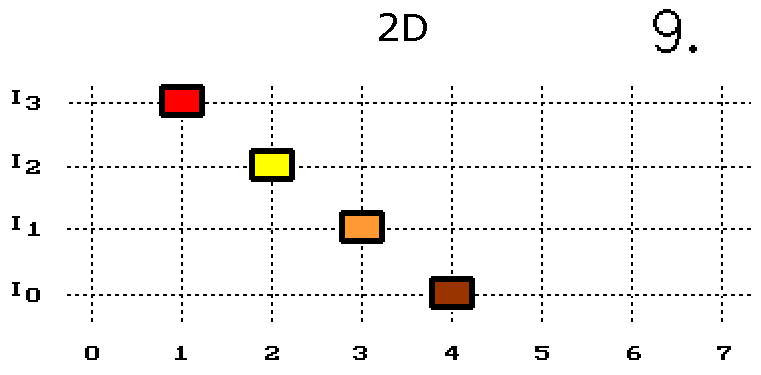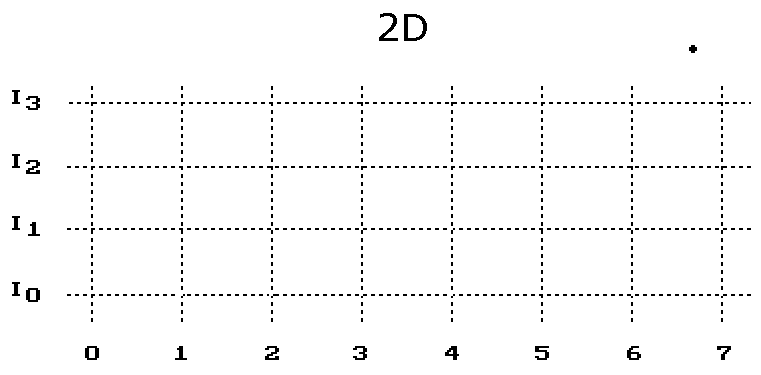
Obr. 2. Otáčení dlouhé úsečky ve 2D prostoru
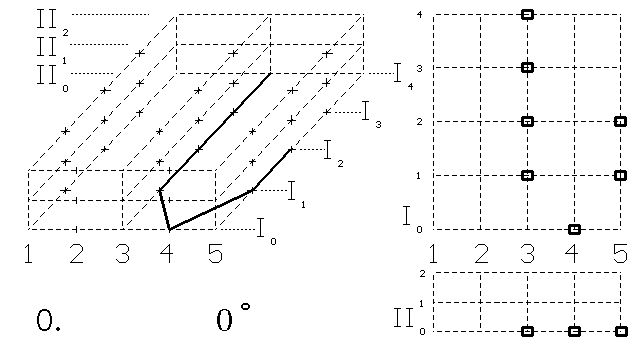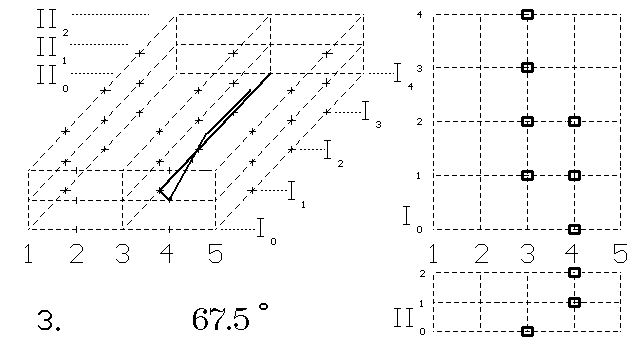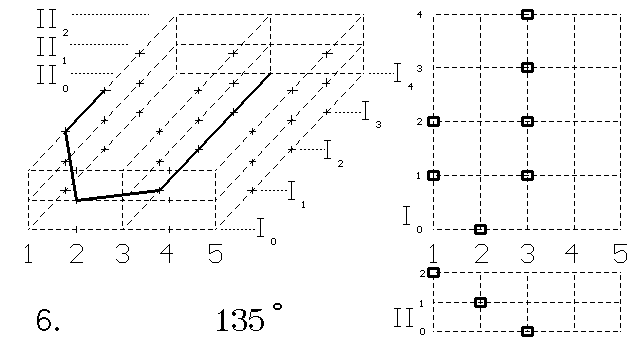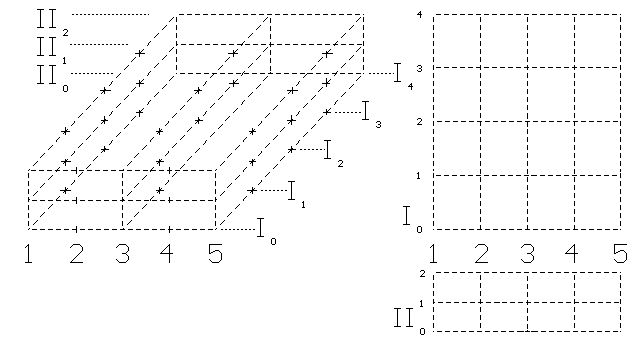
Obr. 3. Otáčení písmene J v 3D objemu. Půdorys a nárys. Vlevo je
ikmý pohled
Dvojrozměrný objekt - špatně napsané písmeno J - otáčejme v objemovém prostoru. Po vrácení na plochu z něho vzniklo správné písmeno J. Opět při otáčení útvaru určeme bodům pohyb po 1 kroku a snažme se dodržovat podobnost s úsečkou Euklidova prostoru.
Představme si úsečku umístěnou na dně krychle. Úsečkou lze otáčet
po ploše té základny; neopustí dno krychle. Ale lze jí také otáčet
s využitím nikoliv 2D prostoru na dně, ale s využitím objemu
krychle. Krajním bodem ať zůstává obsažena ve dně krychle, ale
všechny ostatní body se postupně přemístí do objemu a nakonec
se, otočená, vrátí do dna krychle.
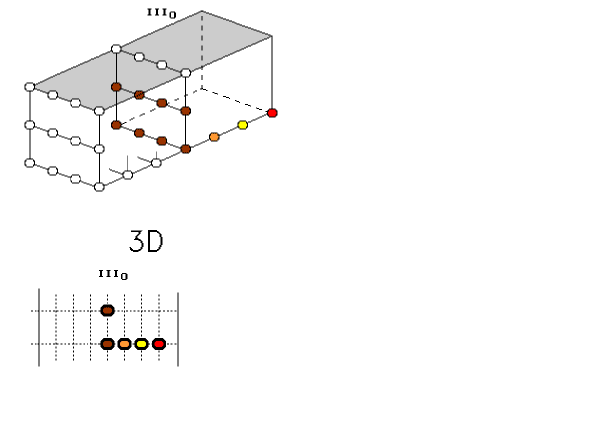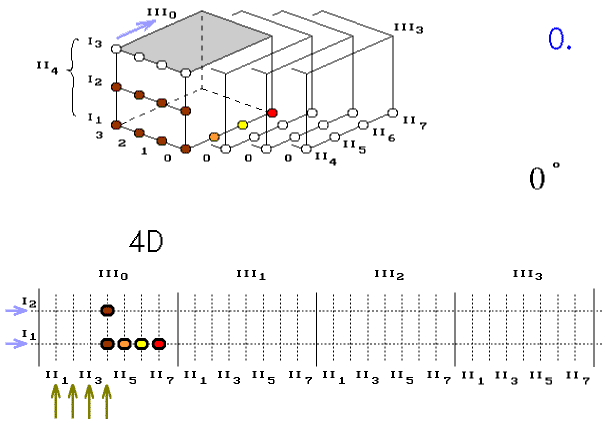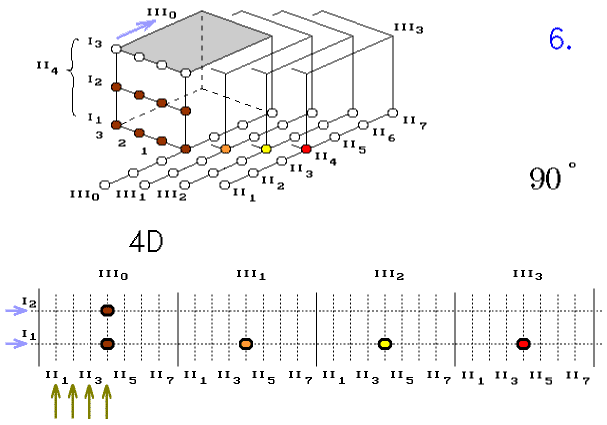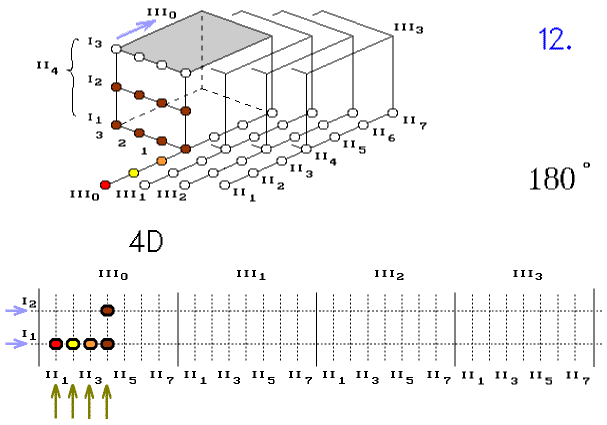
Úsečkou lze tedy otáčet jak v 2D, tak v 3D prostoru. Z toho vychází, že úsečku lze otáčet také s využitím 4D prostoru. Po otočení se vrátí zpět do svého 1D prostoru (obr. 4.).
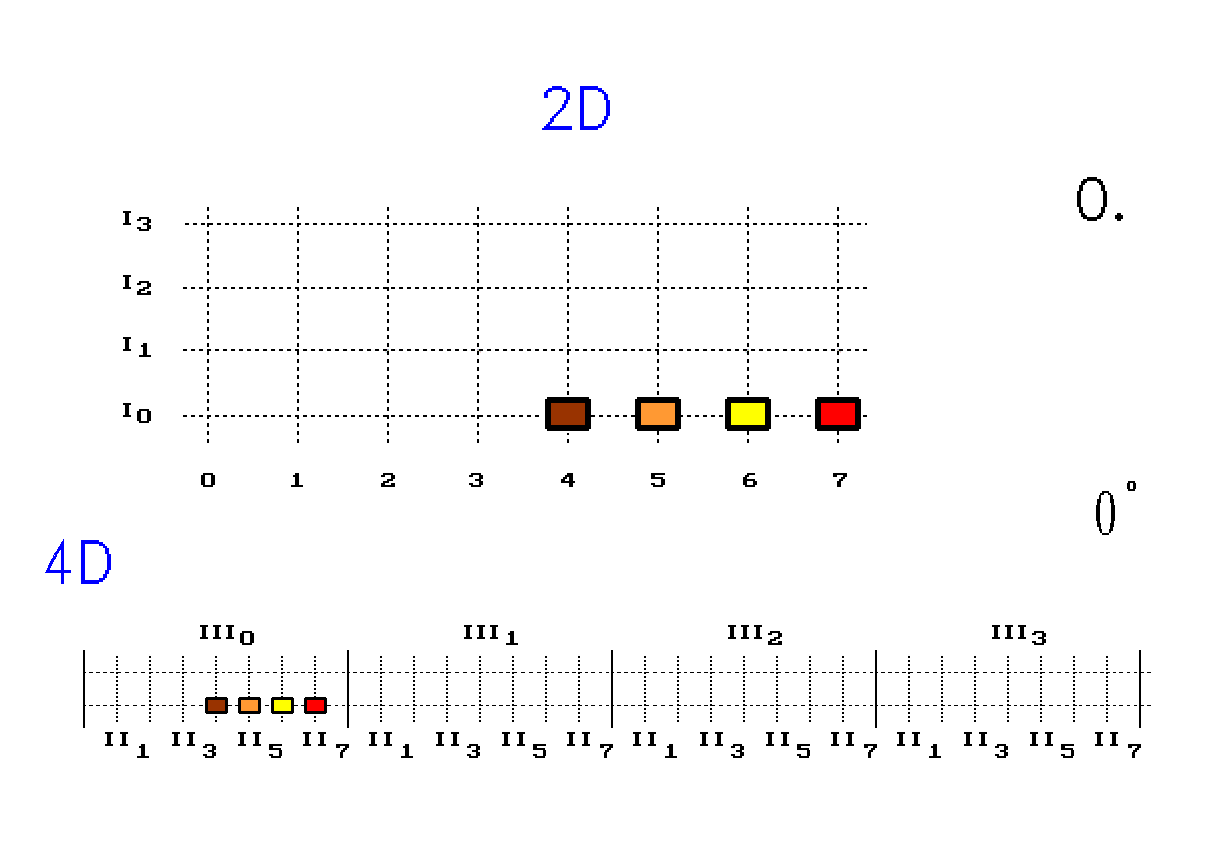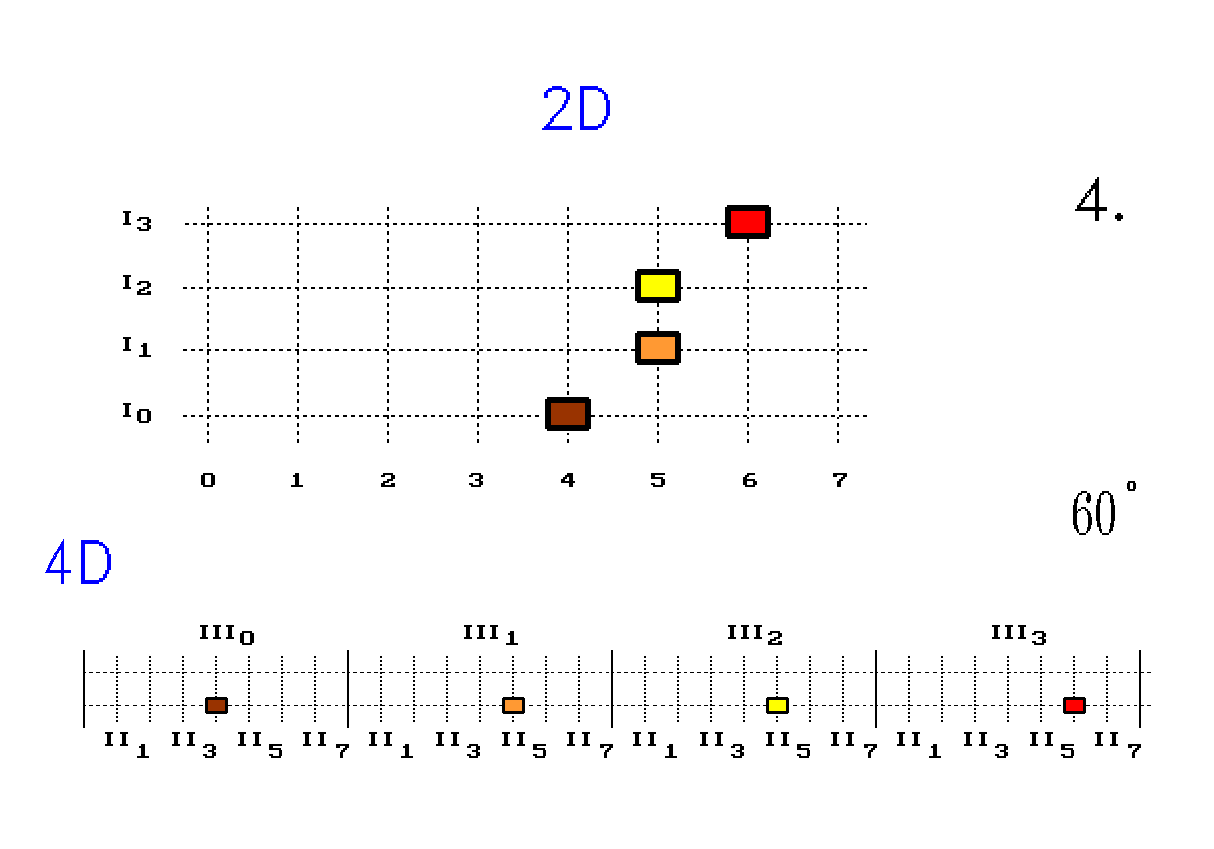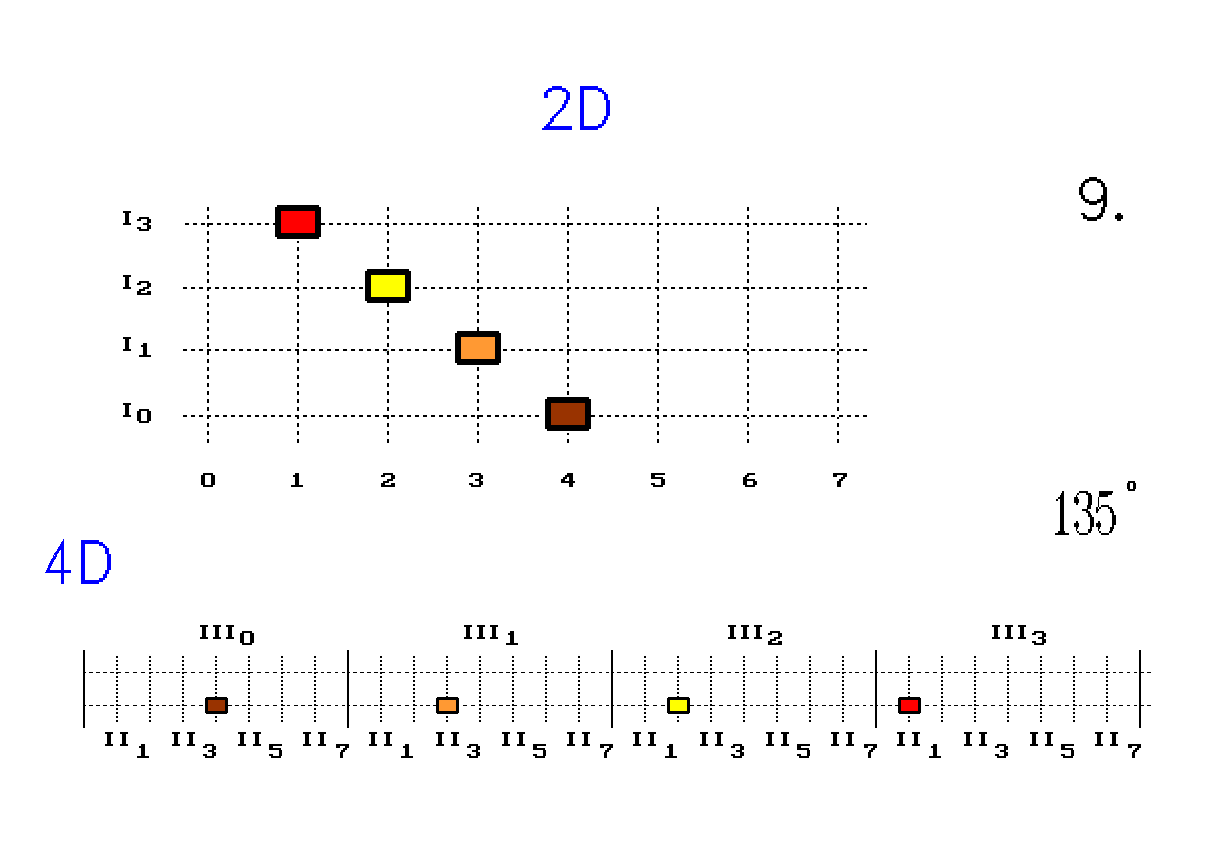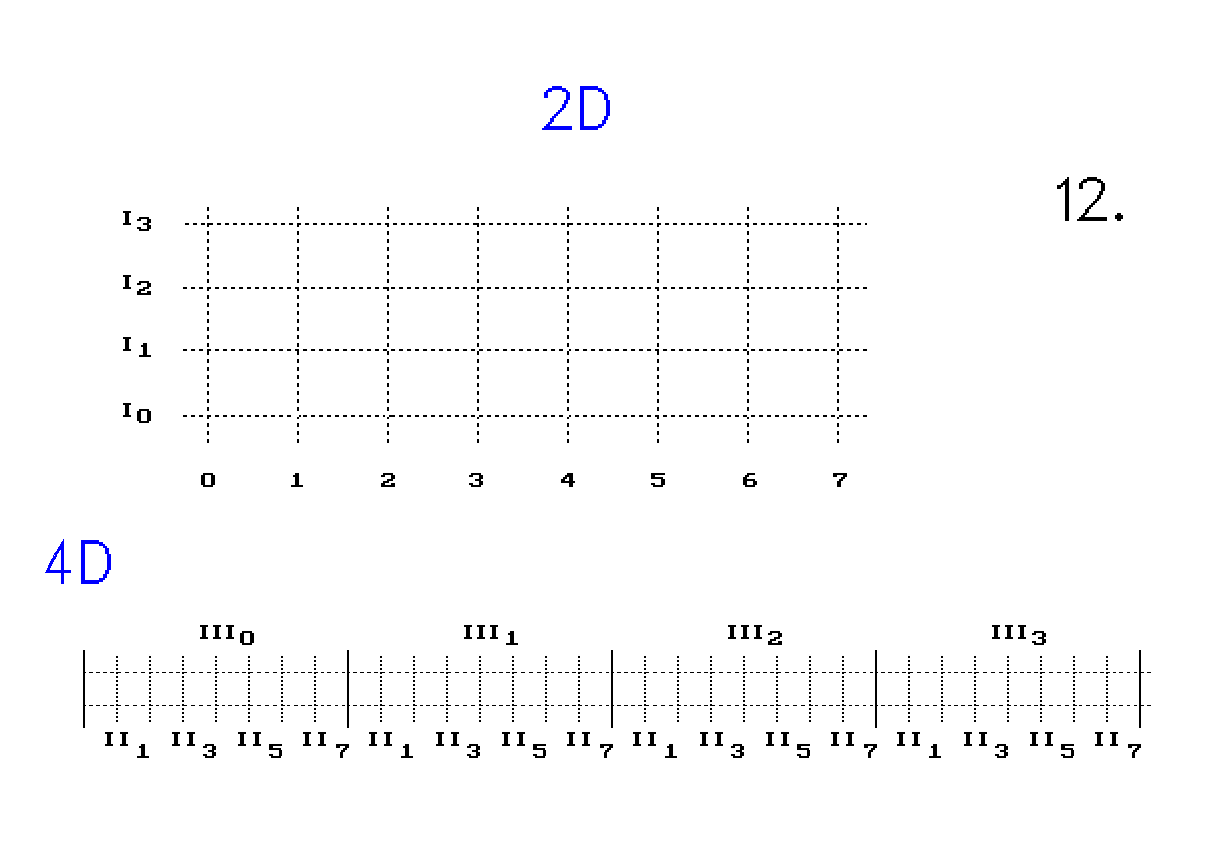
Obr. 4. Otáčení čtyřbodové úsečky využitím 4D prostoru
Nahoře je 2D plocha navrstvená ze čtyř 1D prostorů I0 až I3. Dole je 4D prostor složený ze sousedních objemů III0 až III3.
Horní obrázek 2D slouží jako vzor, ze kterého se odvodí dolní
obrázek
4D. Ukazuje otáčení jakoby s využitím dna krychle.
Dolní obrázek, 4D prostředí, má úsečku na začátku umístěnou v jediném objemu III0. Obdobně, jako když, v horním obrázku, byla úsečka v prostoru I0.
Při otáčení úsečka navštěvuje další objemy. Rozmísťování v plochách, které patří dalším objemům, berme z horního obrázku 2D. Divné údaje, o úhlu ve stupních (např. 105°), pomáhají k orientaci při otáčení diskrétní úsečky.
Nakonec zobrazme otočení objektu - starého obdélníkového stolu,
kterému zbývá jediná noha z původních čtyř (obr. 5.).
Žádným otáčením v objemu nelze jeho poslední nohu přemístit tak,
aby z se posice L přemístila do P - aby při pohledu na spodní stranu
desky stolu se noha nalézala vlevo nahoře namísto vlevo dole. Avšak
otočit stolem lze v hypotetickém 4D prostoru.
Nepoužijme čtvercový stůl; jeho otočením bychom snadno umístili nohu v horním levém bodě P. Nebylo by potřeba otočení ve 4D prostoru.
Obr. 5. Vrak obdélníkového stolu
Stůl je sestavený z 11 bodů. Jeho desku tvoří dva 1D prostory I1
a I2
v rovině II4. Při otáčení ve 4D prostoru se tyto body v
posicích nepřemísťují. Proto v desce stolu, z osmi bodů,
pojmenujme jen dva nejbližší body: E a A.
Při otáčení ve 4D zůstane deska stolu II4
stále ve svém původní objemu III0.
Při prvním zamyšlení člověku připadá, že by se ta noha stolu musela
ukroutit (posice [IV/III0/II4/I1/0]).
Jenže bod je toliko informací, podobně se „kroutil“ při otáčení úsečky
ve 2. obrázku bod v posici [II/I0/4]. Tam nebylo nad čím
přemýšlet, situace nám připadala přijatelná.
Obr. 8. Otočení 3D objektu ve 4D prostoru - zastavený obrázek
Například při otáčení 4D tělesa v 5D prostoru bude osou otáčení 3D těleso.